來源于kb129的博客,版權歸原作者所有:
本來是不想寫的,是因為自己還沒有徹底搞懂唯一的一個環節:軟件實現和理論怎么對應。對于我這種黑白是非必須分明的人而言,這是一種折磨。而這周類似的,懸而未決的事情遠不止這一件。這些導致這周過得很不爽快,但是我很清楚的明白我必須去面對,去接受,去改變,就像昨晚的歐冠,這么虐心的過程,說不定在最后迎來意想不到的大勝利。
循環冗余校驗,也稱為CRC檢驗,這是一個很常見的,很成熟的算法。該算法的理解很簡單,隨便用百度百科一搜,然后花半個小時估計就能完全理解了。這篇博文描述:怎么實現硬件并行的CRC計算。主要的參數為:
1.生成多項式,在不同的協議中有不同的生成多項式,一般這些多項式都是確定的。

2.模2除法
如果已經了解CRC算法,就明白它的原理就是將數據和多項式進行模2除,最后得到的余數就是最后的CRC。這里需要記住的就是:模2除就是進行異或。
但是,如果上面的你都了解后,你會發現這些對于解決CRC算法完全沒有作用,這就是坑爹的百科。網絡上大部分的CRC都是軟件實現,其實在解壓軟件中就有CRC,但是此時又會出現一個問題,你會發現下載的軟件對于同一個字符串,CRC算出來的結果會不同。
這里給一個表示正確的CRC計算軟件:http://www.pc6.com/softview/SoftView_100981.html
軟件界面:
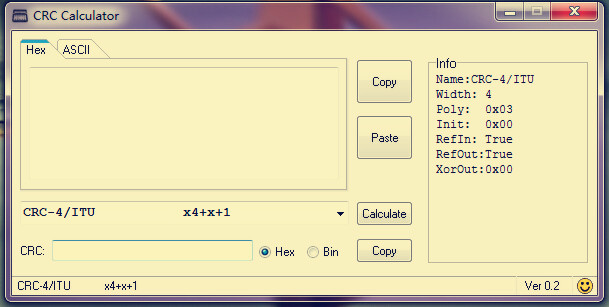
軟件說明 :(作為一個搞硬件的,理解這些軟件參數的確不是一個容易的活,搜了很多資料)
width : 表示最后CRC的bit的位數
Poly : 表示多項式對應的二進制數,這里沒有進行顛倒,x4+x+1=10011,最高位省略,對應的就是0x03,如果顛倒就是0x1100。init :表示軟件寄存器初值,上圖為0x00.
refin : 如果此值為true,表示輸入的數據需要進行比特翻轉,也就是Bit7要變成最低位, Bit0要變成最高位,這里是每個字節而言,每個字節之間的關系不需要進行顛倒。如果此值為false,表明不需要進行字節的比特翻轉
refout:如果此值為true,這表示進行異或后算出來的CRC需要進行整個比特翻轉,然后存入寄存器,例如:123456789 (實際中只能為0,1,為了方便解釋這里的 翻轉和refin的區別,此處6,7,8,9等都是一位),轉換后就是:987654321.如果此值為false,例如:123456789,則該一步后的輸出為123456789
XorOut:最個是將異或后的數據,在refout后的得到的數據與該值進行異或后,最終結果才是軟件計算的CRC。
對于軟件的詳細解釋有:
http://www.cnblogs.com/poiu-elab/archive/2012/10/22/2734715.html
好了,下面是硬件實現。有很多論文都對CRC進行描述,但是其實都是沒有實際作用,但是有一個網站在這一方面做的特別好。鏈接:
http://www.easics.com/webtools/crctool
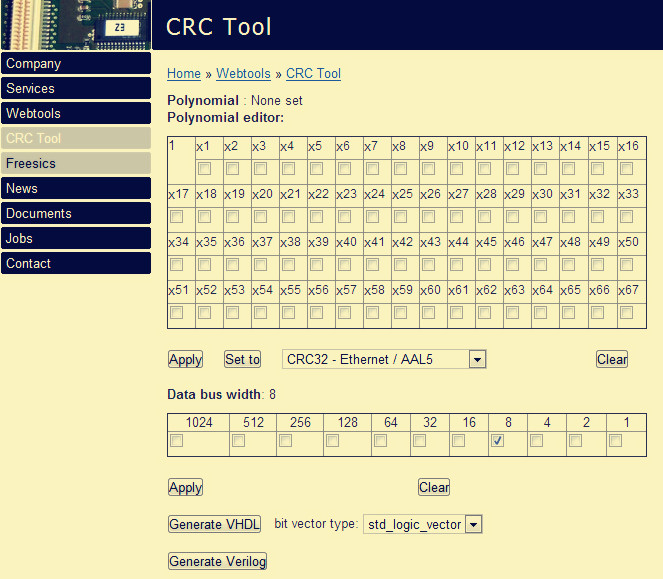
通過該網站,你會等到一個硬件代碼,但是,你會發現這個硬件代碼其實并沒有用。因為代碼僅僅是一個function,并不能直接使用,例如我生成的是CRC32,配置如下:
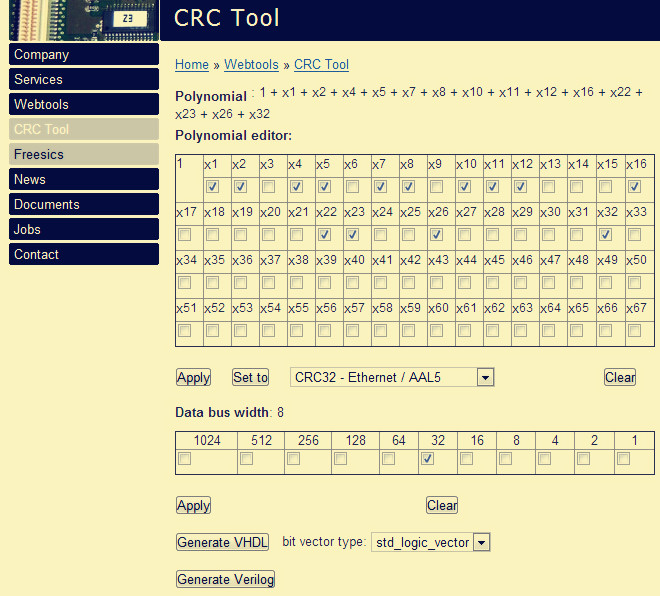
得到的verilog代碼為:
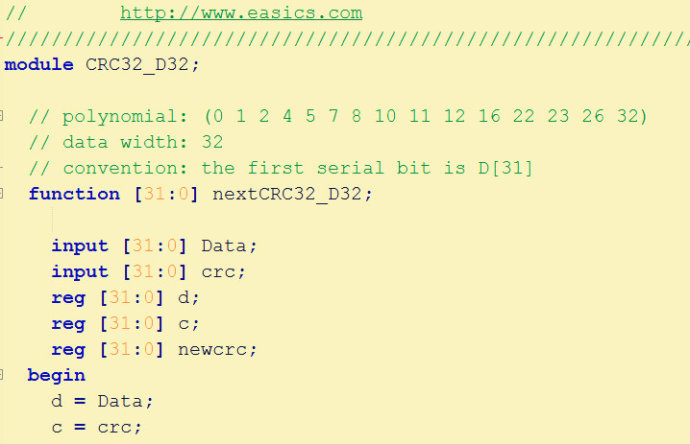
此時就需要修改硬件代碼:
1.首先將代碼從function轉變為時序邏輯電路,也就是添加clk,rst,en。
這一部分由于是教研室代碼,所以不能公布,修改還是很簡單的,只需要花點時間。
2.修改輸入和輸出,這個得根據軟件的配置:
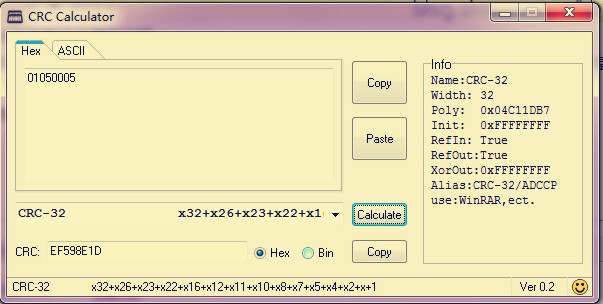
此處的refin,refout,XorOut分別為:true,true,0xFFFFFFFF,也就是輸入需要進行比特翻轉,輸出需要整體比特翻轉,最后需要和0xFFFFFFFF異或,也就是取反(0^1=1 , 1^1=0).
此處修改代碼:輸入比特翻轉

輸出整體翻轉和取反

仿真的結果為:

分析:
可以從仿真圖中看到:如果輸入的是01050005,進行CRC32后的結果為:ef598e1d.對比軟件算出來的結果(上圖的上圖的上圖的上圖):EF598E1D。可見兩者算出來的結果是一樣的。
最后給出我還沒有理解的問題:為何上面的計算結果和我們自己用筆在紙上計算的CRC不一樣呢?
描述:
情況一:當refin 和refout都為true
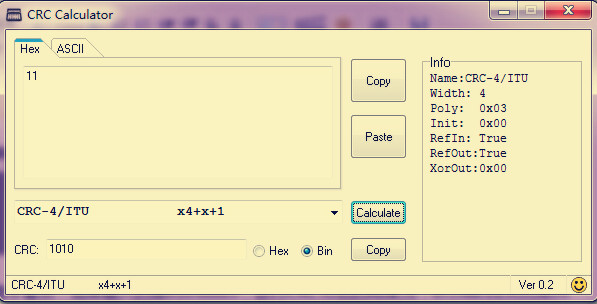
而此手算結果為:

此時的計算值和軟件算出來的值,不一樣,就是不清楚軟件那邊是怎么個翻轉
情況二:當refin 和refout都為false
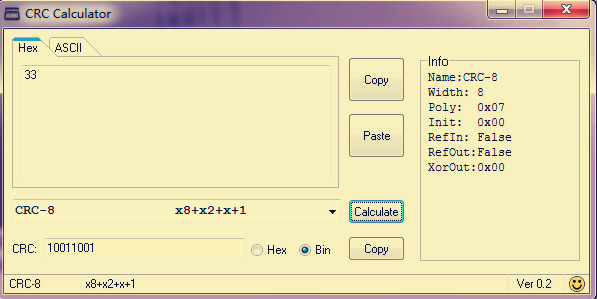
手算的結果:

對比發現,手算和軟件計算是一樣的,所以總結出來問題:
就是在需要bit翻轉和整體翻轉的時候,軟件計算算出來的CRC是什么字符串的CRC呢?
PS : 在無意瀏覽網頁的時候,發現了一個更好的硬件CRC生成網站,但是我沒有對代碼進行測試。鏈接為:http://outputlogic.com/?page_id=321













