筆試面試的過程中難免會遇到很多自己不清楚或者是當時不清楚的問題,關于浮點型數據的問題我認為是比較難的問題啦,如果不清楚浮點型存儲問題,回答問題只有猜結果了。
在面試的過程中一般面試官也很少問關于浮點數的問題,因為浮點數對于很多的處理器是不支持的,對于上層應用的程序員而言,存儲類型的問題都會考慮,但是對于嵌入式程序員掌握內存的分配情況是必須的,只有這樣才能把握基本的操作,關于浮點型數據,在C語言中存在兩種類型的浮點型,其中一種是單精度的浮點型 (float)、雙精度的浮點型(double)。浮點型數據和一般的整形數據具有較大的差別,具體的差別就是浮點型數據是一個近似值,并不是一個準確的值,這也就是為什么在比較浮點型數據的大小時不能采用直接等于的方式進行比較,因為浮點型只是一個近似值,也就是一個值可能表示一個范圍區間,這樣的表達方式就使得對浮點型采用相等的判斷方法進行判斷可能不合理,只有通過比較一個數是否在這個小的范圍內,在這個小的范圍內說明這個數可以表述這個范圍內的數據。因此在計算值比較兩個浮點數變量不能通過做差是否等于零來判斷。而只能通過如下的方式判斷:
- const float ESPSION = 0.000001;
- if((x-y)>=-ESPSION && (x-y)<= ESPSION)
這種實現方式是基本的比較方式,這種判讀方法剛好就是判斷變量是否處于一個范圍內,這里的范圍是-0.000001<x<0.000001。
記得在網上關于浮點型的一道題目如下:
typedef union test
{
float a;
int i;
char c[4];
}Test;
{
float a;
int i;
char c[4];
}Test;
int main()
{
Test t;
t.a = 5.0;
printf("%f\n",t.a)
printf("%d\n",t.i);
printf("%c,%c,%c,%c\n",t.c[3],t.c[2],t.c[1],t.c[0]);
return 0;
}
{
Test t;
t.a = 5.0;
printf("%f\n",t.a)
printf("%d\n",t.i);
printf("%c,%c,%c,%c\n",t.c[3],t.c[2],t.c[1],t.c[0]);
return 0;
}
其實關于數據類型的存儲方式問題的題目類型很多,其中比較常見的有:1、存儲空間大小問題,即字節對齊問題,這種問題一般要求我們對基本類型了解其中的基本原理,相對來說比較簡單。2、字符串的長度問題,這種問題主要是通過sizeof,strlen這兩個不同的函數來比較。3、還有一類問題就是采用 printf函數實現數據類型的轉換問題。這種轉化問題是在printf的格式中體現出來的,是各種關于內存分布最容易失誤的地方,為什么說最容易失誤呢,因為不同的參數就有可能產生不一樣的輸出結果,說白了這種題很容易出錯是因為我們很少注意這些問題。
上面的這個題返回值非常的特殊,為什么會特殊呢?我就通過浮點數的基本存儲方式來說明。在32位系統中,float類型占有4個bytes,double 則占有8個bytes。對于整形數據而言,我們很容易就知道數據是順序存儲的,雖然有大小端之分,但是基本的準則我們認為是按照順序存儲的。但是 float和double型卻是比較特殊的數據類型,因為這兩種數據類型并不是按照整形數據的順序存儲方式進行存儲的,而是按照一定的標志IEEE來實現的,都有各自的標志編碼方式:
浮點型變量在計算機內存中占用4字節(Byte),即32-bit。遵循IEEE-754格式標準。一個浮點數由2部分組成:底數m 和指數e。
±mantissa × 2^exponent
(注意,公式中的mantissa 和 exponent使用二進制表示)
(具體可參看深入理解計算機系統)
底數部分 使用2進制數來表示此浮點數的實際值。
指數部分 占用8-bit的二進制數,可表示數值范圍為0-255。但是指數應可正可負,所以IEEE規定,此處算出的次方(即是來自內存存儲的內容,存儲指數)須減去127才是真正的指數(實際的指數,如12.5轉換為二進制為:1100.100=1.100100*23, 3即為實際指數)。所以float的指數可從 -126到128.
底數部分實際是占用24-bit的一個值,由于其最高位始終為1,所以最高位省去不存儲,在存儲中只有23-bit。到目前為止,底數部分23位加上指數部分8位使用31位。那么前面說過,float是占用4個字節即32-bit, 那么還有一位是干嘛用的呢? 還有一位,其實就是4字節中的最高位,用來指示浮點數的正負,當最高位是1時,為負數,最高位是0時,為正數。
也就是說我們可以認為float在小端CPU的編碼方式應該是:
31<-------------------------------------------------0
S(1bit)| E(8bits)| M(23bits) |
即:
-----------------------------------------------------
ADDR0+3 ADDR0+2 ADDR0+1 ADDR0
ADDR0+3 ADDR0+2 ADDR0+1 ADDR0
SEEEEEEE EMMMMMMM MMMMMMMM MMMMMMMM
-----------------------------------------------------
S: 表示浮點數正負,1為負數,0為正數。
E: 指數加上127后的值的二進制數
M: 24-bit的底數(只存儲23-bit)
需要注意,浮點數為0時,指數和底數都為0,但此前的公式不成立。因為2的0次方為1,所以,0是個特例。當然,這個特例也不用認為去干擾,編譯器會自動去識別。
這樣我們就可以知道前面這個題中輸出的結果啦,從上面的分析可以知道一個float型的數的基本存儲方式,按照上面的實現可以知道5.0的存儲方式為如下的形式:
01000000101000000000000000000000
從上面的這個存儲形式我們可以得到基本的整形數值時0x40A00000。進而也就知道了4個bytes中的數值大小。
這是充分利用了聯合體的共享內存特性,我們改變程序如下所示:
#include<stdio.h>
typedef union test
{
float a;
int i;
char c[4];
}Test;
{
float a;
int i;
char c[4];
}Test;
int main()
{
Test t;
t.a = 5.0;
printf("%f\n",t.a);
printf("%d\n",t.i);
printf("%c,%c,%c,%c\n",t.c[3],t.c[2],t.c[1],t.c[0]);
{
Test t;
t.a = 5.0;
printf("%f\n",t.a);
printf("%d\n",t.i);
printf("%c,%c,%c,%c\n",t.c[3],t.c[2],t.c[1],t.c[0]);
t.i = 65;
printf("%f\n",t.a);
printf("%d\n",t.i);
printf("%c,%c,%c,%c\n",t.c[3],t.c[2],t.c[1],t.c[0]);
return 0;
}
printf("%f\n",t.a);
printf("%d\n",t.i);
printf("%c,%c,%c,%c\n",t.c[3],t.c[2],t.c[1],t.c[0]);
return 0;
}
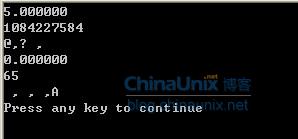
根據上面的分析,可以比較方便的計算出結果如下所示:
當然這只是我在X86系統中的輸出,在大端系統中會是什么結果我不得而知,具體的要參看IEEE標準。
float類型的數據是比較復雜的問題,我將在后面認真研究,爭取早日解決各種問題。