引言
在數字計算中,加、減、乘、除運算經常使用。在FPGA中,有加、減、乘、除的算法指令,但除法中除數必須為2的冪,因此無法實現除數為任意數的除法;而二進制除法算法中包含了減法、乘法、數的分解與合成、試商的判斷等多種操作過程。因此,除法運算過程非常復雜,用VHDL編寫除法運算很難實現。因此,作者根據二進制乘法的原理,采用被除數與除數的倒數相乘的方法來實現二進制的除法。
1 十六位二進制乘法
二進制乘法是通過逐項移位相加原理來實現的。從被乘數的最低位開始,若為1,則乘數左移后送入寄存器進行累加;若為0,左移后以全零相加。如此往復,直至被乘數的最高位。乘法運算結束后,此時累加器中的輸出值即為最后的積。圖1所示為乘法原理框圖。
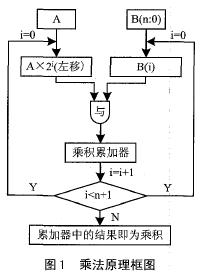
圖1 乘法原理框圖
根據上述原理,設計VHDL算法,實現十六位二進制乘法。乘法在一個時鐘周期內完成。
LIBRARY IEEE;
USE IEEE.STD_LOGIC_1164.ALL;
USE IEEE.STD_LOGIC_UNSIGNED.ALL;
ENTITY MULTIPLY IS
PORT(CLK:IN STD_LOGIC;
A:IN STD_LOGIC_VECTOR(15 DOWNTO 0);
//乘數
B:IN STD_LOGIC_VECTOR(15 DOWNTO 0);
//被乘數
START:IN STD_LOGIC;
CH:OUT STD_LOGIC_VECTOR(15 DOWNTO 0);
CL:OUT STD_LOGIC_VECTOR(15 DOWNTO O));
END MULTIPLY;
ARCHITECTURE BEHAV OF MULTIPLY IS
SIGNAL L8:STD_LOGIC_VECTOR(15 DOWNTO O);
BEGIN
PROCESS(CLK)
VARIABLE ACC:STD_LOGIC_VECTOR(31 DOWNTO 0);
VARIABLE N:STD_LOGIC_VECTOR(7 DOWNTO 0);
VARIABLE Q:STD_LOGIC_VECTOR(31 DOWNTO O);
VARIABLE MA:STD_LOGIC_VECTOR(31 DOWNTO O);
BEGIN
IF START='1'THEN
IF CLK'EVENT AND CLK='1'THEN
MA(31 DOWNTO 0):="0000000000000000"&A(15
DOWNTO 0);
ACC:="00000000000000000000000000000000";
FOR I IN 0 TO 15 LOOP
FOR JIN 0 TO 31 LOOP
Q(J):=B(I) AND MA(J); //B(I)與MA相"與"
END LOOP;
ACC:=ACC+Q; //累加
MA(31 DOWNTO 0):=MA(30 DOWNTO 0)&MA(31);
//左移
ENDLOOP;
CH<=ACC(31 downto 16); //乘積的高16位
CL<=ACC(15 downto 0); //乘積的低16位
ENDIF;
ENDIF;
END PROCESS;
END BEHAV;
綜合后生成的乘法器宏如圖2所示。
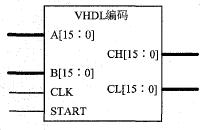
圖2二進制乘法器
2 二進制除法的改進
由于在FPGA中實現二進制除法的算法十分復雜,我們在實現二進制除法時,采取被除數與除數的倒數相乘的方法。因此,在給定除數的同時必須計算出除數的倒數,由于除數的倒數是小數形式(除數為1時,倒數為1),因此我們將此倒數的小數部分的16位和整數部分的最后1位(主要考慮除數為1時,倒數的整數部分為1)記錄成17位二進制。這樣可以與被除數進行二進制乘法運算。乘積的后16位為商的小數部分。前面為商的整數部分。
在FPGA中,我們將除數作為寄存器的地址,其倒數的小數部分作為寄存器的內容。這樣,再計算除數的倒數,就相當于一次寄存器的尋址。圖3為改進的除法原理框圖。
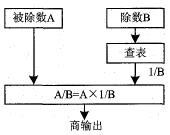
圖3改進的除法原理框圖
用VHDL設計的查表程序如下(它可在一個時鐘周期內將除數B轉換成1/B,輸出結果M的低16位為倒數的小數部分,M的第17位為倒數的整數部分):
LIBRARY IEEE;
USE IEEE.STD_LOGIC_1164.ALL;
ENTITY TABLE IS
PORT(
N:IN STD_LOGIC_VECTOR (7 downto 0);
CLK:IN STD_LOGIC;
READ:IN STD_LOGIC;
M:out STD_LOGIC_VECTOR(16 downto 0)//倒數的
//整數M(16)和小數部分M(15:0)
);
END TABLE;
ARCHITECTURE TABLE_ARCH OF TABLE IS
SIGNAL L8:STD_LOGIC_VECTOR(16 DOWNTO 0);
BEGIN
PROCESS(CLK,READ)
IF READ='l'THEN
IF CLK'EVENT AND CLK='l'THEN
WHEN"00000001"=>L8<="10000000000000000";
WHEN"00000010"=>L8<="01000000000000000";
WHEN"00000011"=>L8<="00101010101010101";
WHEN"00000100"=>L8<="00100000000000000";
WHEN"00000101"=>L8<="00011001100110011";
WHEN"00000110"=>L8<="00010101010101010";
WHEN"00000111"=>L8<="00010010010010010";
WHEN"11111001"=>L8<="00000000100000111";
WHEN"11111010"=>L8<="00000000100000110";
WHEN"11111011"=>L8<="00000000100000101";
WHEN"11111100"=>L8<="00000000100000100";
WHEN"11111101"=>L8<="00000000100000011";
WHEN"11111110"=>L8<="00000000100000010";
WHEN"11111111"=>L8<="00000000100000001";
WHEN OTHERS=>L8<="ZZZZZZZZZZZZZZZZZ";
//以上為1-255的倒數
END CASE;
M<=L8;
ENDIF;
ENDIF;
END PROCESS;
END TABLE_ARCH;
綜合后生成倒數轉換寄存器的宏如圖4所示。
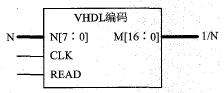
圖4除數轉化其倒數寄存器
用原理圖將上面所生成的宏連接成完整的除法器如圖5所示。其中A[15:0]為被除數,B[7:0]為除數,c[31:16]為商的整數部分,C[15:0]為商的小數部分。
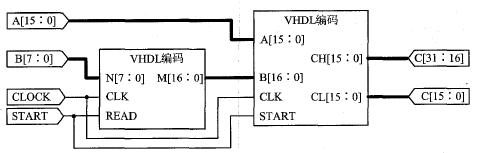
圖5 完整的二進制除法器
我們選擇幾對被除數和除數進行了仿真,其結果如圖6和表1所示。
表1部分仿真結果
| 被除數 | 除數 | 商的整數部分 | 商的小數部分 |
| 0450 | 68 | 000A | 9CE0 |
| 0036 | 68 | 0000 | 84E4 |
| 0256 | 68 | 0005 | BFA4 |
| 0256 | 39 | 000A | 7BFE |
| 0168 | 17 | 000F | A668 |
結語
應用上述的二進制乘法和二進制除法,我們解決了工程中所需的乘法和除法運算問題。其中除法運算的商可以精確到小數點后面16位,達到了工程中對運算精度的要求。二進制乘法可以擴展到任意位數,二進制除法中被除數可以為任意位數。由于本方法中除數轉換為其倒數的過程是由作者手工輸入,并作為寄存器的內容進行存儲的, 因此只考慮了除數為8位的情況,當然,也可以完成更高位的寄存器尋址,但工作量很大。
