|
不管多么經典的射頻教程,為什么都做成黑白的呢?讓想理解史密斯原圖的同學一臉懵逼。

這是什么東東?
今天解答三個問題: 1、是什么? 2、為什么? 3、干什么?
1、是什么? 該圖表是由菲利普·史密斯(Phillip Smith)于1939年發明的,當時他在美國的RCA公司工作。史密斯曾說過,“在我能夠使用計算尺的時候,我對以圖表方式來表達數學上的關聯很有興趣”。 史密斯圖表的基本在于以下的算式。
當中的Γ代表其線路的反射系數(reflection coefficient) 即S參數(S-parameter)里的S11,ZL是歸一負載值,即ZL / Z0。當中,ZL是線路本身的負載值,Z0是傳輸線的特征阻抗(本征阻抗)值,通常會使用50Ω。 簡單的說:就是類似于數學用表一樣,通過查找,知道反射系數的數值。
2、為什么? 我們現在也不知道,史密斯先生是怎么想到“史密斯圓圖”表示方法的靈感,是怎么來的。
很多同學看史密斯原圖,屎記硬背,不得要領,其實沒有揣摩,史密斯老先生的創作意圖。
我個人揣測:是不是受到黎曼幾何的啟發,把一個平面的坐標系,給“掰彎”了。 我在表述這個“掰彎”的過程,你就理解,這個圖的含義了。(坐標系可以掰彎、人盡量不要“彎”;如果已經彎了,本人表示祝福)
現在,我就掰彎給你看。
世界地圖,其實是一個用平面表示球體的過程,這個過程是一個“掰直”。
史密斯原圖,巧妙之處,在于用一個圓形表示一個無窮大的平面。
2.1、首先,我們先理解“無窮大”的平面。 首先的首先,我們復習一下理想的電阻、電容、電感的阻抗。
在 具有電阻、電感和電容的電路里,對電路中的電流所起的阻礙作用叫做阻抗。阻抗常用Z表示,是一個復數,實際稱為電阻,虛稱為電抗,其中電容在電路中對交流 電所起的阻礙作用稱為容抗 ,電感在電路中對交流電所起的阻礙作用稱為感抗,電容和電感在電路中對交流電引起的阻礙作用總稱為電 抗。 阻抗的單位是歐姆。
R,電阻:在同一電路中,通過某一導體的電流跟這段導體兩端的電壓成正比,跟這段導體的電阻成反比,這就是歐姆定律。 標準式: 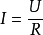 。(理想的電阻就是 實數,不涉及復數的概念)。 。(理想的電阻就是 實數,不涉及復數的概念)。
如果引入數學中復數的概念,就可以將電阻、電感、電容用相同的形式復阻抗來表示。既:電阻仍然是實數R(復阻抗的實部),電容、電感用虛數表示,分別為:
Z= R+i( ωL–1/(ωC)) 說明:負載是電阻、電感的感抗、電容的容抗三種類型的復物,復合后統稱“阻抗”,寫成數學公式即是:阻抗Z= R+i(ωL–1/(ωC))。其中R為電阻,ωL為感抗,1/(ωC)為容抗。 (1)如果(ωL–1/ωC) > 0,稱為“感性負載”; (2)反之,如果(ωL–1/ωC) < 0稱為“容性負載”。
我們仔細看阻抗公式,它不再是一個實數。它因為電容、電感的存在,它變成了一個復數。 
電路中如果只有電阻,只影響幅度變化。
我們通過上圖,我們知道,正弦波的幅度發生了變化,同時,相位也發生了變化,同時頻率特性也會變化。所以我們在計算的過程中,即需要考慮實部,也需要考慮虛部。
我們可以在一個復平面里面,以實部為x軸、以虛部為y軸,表示任意一個復數。我們的阻抗,不管多少電阻、電容、電感串聯、并聯,之后,都可以表示在一個復平面里面。 在 RLC 串聯電路中,交流電源電壓 U = 220 V,頻率 f = 50 Hz,R = 30 Ω,L =445 mH,C =32 mF。 

在上圖中,我們看到通過幾個矢量的疊加,最終阻抗在復平面中,落在了藍色的圓點位置。所以,任意一個阻抗的計算結果,我們都可以放在這個復平面的對應位置。 各種阻抗的情況,組成了這個無窮大的平面。
2.2、反射公式 信 號沿傳輸線向前傳播時,每時每刻都會感受到一個瞬態阻抗,這個阻抗可能是傳輸線本身的,也可能是中途或末端其他元件的。對于信號來說,它不會區分到底是什 么,信號所感受到的只有阻抗。如果信號感受到的阻抗是恒定的,那么他就會正常向前傳播,只要感受到的阻抗發生變化,不論是什么引起的(可能是中途遇到的電 阻,電容,電感,過孔,PCB轉角,接插件),信號都會發生反射。 錢塘江大潮,就是河道的寬度變化引起了反射,這跟電路中阻抗不連續,導致信號反射,可以類比。反射聚集的能量疊加在一起,引起的過沖。也許這個比喻不恰當,但是挺形象。  那么有多少被反射回傳輸線的起點?衡量信號反射量的重要指標是反射系數,表示反射電壓和原傳輸信號電壓的比值。 那么有多少被反射回傳輸線的起點?衡量信號反射量的重要指標是反射系數,表示反射電壓和原傳輸信號電壓的比值。反射系數定義為:
其中:Z0為變化前的阻抗,ZIN為變化后的阻抗。假設PCB線條的特性阻抗為50歐姆,傳輸過程中遇到一個100歐姆的貼片電阻,暫時不考慮寄生電容電感的影響,把電阻看成理想的純電阻,那么反射系數為:
信號有1/3被反射回源端。
如果傳輸信號的電壓是3.3V電壓,反射電壓就是1.1V。 純電阻性負載的反射是研究反射現象的基礎,阻性負載的變化無非是以下四種情況:阻抗增加有限值、減小有限值、開路(阻抗變為無窮大)、短路(阻抗突然變為0)。
初始電壓,是源電壓Vs(2V)經過Zs(25歐姆)和傳輸線阻抗(50歐姆)分壓。 Vinitial=1.33V 后續的反射率按照反射系數公式進行計算 源端的反射率,是根據源端阻抗(25歐姆)和傳輸線阻抗(50歐姆)根據反射系數公式計算為-0.33; 終端的反射率,是根據終端阻抗(無窮大)和傳輸線阻抗(50歐姆)根據反射系數公式計算為1; 我們按照每次反射的幅度和延時,在最初的脈沖波形上進行疊加就得到了這個波形,這也就是為什么,阻抗不匹配造成信號完整性不好的原因。
那么我們做一個重要的假設! 為了減少未知參數的數量,可以固化一個經常出現并且在應用中經常使用的參數。這里Z0 (特性阻抗)通常為常數并且是實數,是常用的歸一化標準值,如50Ω、75Ω、100Ω和600Ω。 假設Z0一定,為50歐姆。(為什么是50歐姆,此處暫時不表;當然也可以做其他假設,便于理解,我們先定死為50Ω)。 那么,根據反射公式,我們得到一個重要的結論: 
每一個Zin對應唯一的 “Γ”,反射系數。我們把對應關系描繪到剛剛我們說的“復平面”。 于是我們可以定義歸一化的負載阻抗:

據此,將反射系數的公式重新寫為:

好了,我們在復平面里面,忘記Zin,只記得z(小寫)和反射系數“Γ”。 準備工作都做好了,下面我們準備“彎了” 2.3 掰彎 
在復平面中,有三個點,反射系數都為1,就是橫坐標的無窮大,縱坐標的正負無窮大。歷史上的某天,史密斯老先生,如有神助,把黑色線掰彎了,把上圖中,三個紅色圈標注的點,捏到一起。
彎了,彎了 
圓了,圓了。
完美的圓:
雖然,無窮大的平面變成了一個圓,但是,紅線還是紅線,黑線還是黑線。
同時我們在,原來的復平面中增加三根線,它們也隨著平面閉合而彎曲。
黑色的線上的阻抗,有個特點:實部為0;(電阻為0)
紅色的線上的阻抗,有個特點:虛部為0;(電感、電容為0) 綠色的線上的阻抗,有個特點:實部為1;(電阻為50歐姆) 紫色的線上的阻抗,有個特點:虛部為-1; 藍色的線上的阻抗,有個特點:虛部為1; 
線上的阻抗特性,我們是從復平面,平移到史密斯原圖的,所以特性跟著顏色走,特性不變。


下半圓與上班圓是一樣的劃分。
因為史密斯圓圖是一種基于圖形的解法,所得結果的精確度直接依賴于圖形的精度。下面是一個用史密斯圓圖表示的RF應用實例:
例: 已知特性阻抗為50Ω,負載阻抗如下:
| Z1 = 100 + j50Ω | Z2 = 75 - j100Ω | Z3 = j200Ω | Z4 = 150Ω | | Z5 = ∞ (an open circuit) | Z6 = 0 (a short circuit) | Z7 = 50Ω | Z8 = 184 - j900Ω |
對上面的值進行歸一化并標示在圓圖中(見圖5):
| z1 = 2 + j | z2 = 1.5 - j2 | z3 = j4 | z4 = 3 | | z5 = 8 | z6 = 0 | z7 = 1 | z8 = 3.68 - j18 |
我們看不清上圖。 如果是“串聯”,我們可以在清晰的史密斯原圖上,先確定實部(紅線上查找,原來復平面的橫坐標),再根據虛部的正負,順著圓弧滑動,找到我們對應的阻抗。(先忽略下圖中的綠色線) 
現在可以通過圓圖直接解出反射系數Γ。我們既可以通過直角坐標,去直接讀取反射系數的值,也可以通過極坐標,讀取反射系數的值。 直角坐標 畫出阻抗點(等阻抗圓和等電抗圓的交點),只要讀出它們在直角坐標水平軸和垂直軸上的投影,就得到了反射系數的實部Γr和虛部Γi (見圖6)。
該范例中可能存在八種情況,在圖6所示史密斯圓圖上可以直接得到對應的反射系數Γ:
| Γ1 = 0.4 + 0.2j | Γ2 = 0.51 - 0.4j | Γ3 = 0.875 + 0.48j | Γ4 = 0.5 | | Γ5 = 1 | Γ6 = -1 | Γ7 = 0 | Γ8 = 0.96 - 0.1j |
從X-Y軸直接讀出反射系數Γ的實部和虛部
極坐標
極坐標表示,有什么用?非常有用,這其實也是史密斯原圖的目的。
2.4 紅色陣營VS綠色陣營 剛剛我們已經注意到,史密斯原圖,除了有紅色的曲線,是從阻抗復平面掰彎,過來的紅色世界。同時,在圖中,還有綠色的曲線,他們是從導納復平面,掰彎產生的。過程跟剛剛的過程是一樣的。 那么這個導納的綠色,有什么用呢? 并聯電路,用導納計算,我們會很便利。同時在史密斯原圖中,我們用導納的綠色曲線進行查詢,也會很方便。

如圖,這樣并聯一個電容,通過綠色的曲線很快就可以查詢到對應的歸一化阻抗和反射系數。
3、干什么? 解釋和介紹了史密斯圓圖這么長的段落,別忘了,我們想干什么。我們實際是希望,我們設計的電路反射系數越接近0越好。 但是,什么樣的電路是合格的電路呢?反射系數不可能理想的為0,那么我們對反射系數,有什么樣的要求呢? 我們希望反射系數的絕對值小于1/3,即反射系數落入史密斯圓圖的藍色區域中(如下圖)。

這個藍色的球,有什么特色呢?其實我們通過史密斯原圖的數值已經清楚的發現。在中軸線,也就是之前說的紅線上,分別是25歐姆,和100歐姆兩個位置。即:Zin在1/2 Zo和2倍Zo之間的區域。也就是,我們打靶打在藍色區域,即認為反射系數是可以接受的。 |