摘要

隨著信息時代和數(shù)字世界的到來，數(shù)字信號處理已成為今一門極其重要的學(xué)科和技術(shù)領(lǐng)域。數(shù)字濾波器是數(shù)字信號處理的基礎(chǔ)，用來對信號進行過濾、檢測與參數(shù)估計等處理，在通信、圖像、語音、雷達等許多領(lǐng)域都有著十分廣泛的應(yīng)用。尤其在圖像處理、數(shù)據(jù)壓縮等方面取得了令人矚目的進展和成就。鑒于此，數(shù)字濾波器的設(shè)計就顯得尤為重要。例如，在電力系統(tǒng)微機保護和二次控制中，很多信號的處理與分析都是基于對正弦基波和某些整次諧波的分析，而在系統(tǒng)電壓電流信號（尤其是故障舜變過程）中各種復(fù)雜成分，所以濾波器一直是電力系統(tǒng)二次裝置的關(guān)鍵部件。目前微機保護和二次信號處理軟件主要是采用的數(shù)字濾波器。

目前數(shù)字濾波器的設(shè)計有許多現(xiàn)成的高級語言設(shè)計程序，但他們都存在設(shè)計效率低，不具有可視圖形，不便于參數(shù)修改等缺點，而MATLAB的FDATool工具為數(shù)字濾波器的研究和應(yīng)用提供了一個直觀、高效、便捷的利器。它以矩陣運算為基礎(chǔ)，把計算、可視化、仿真設(shè)計融合到一個交互式的工作環(huán)境中。尤其是MATLAB工具箱使各個領(lǐng)域的研究人員可以直觀方便地進行科學(xué)研究和工程應(yīng)用。其中的信號處理、圖像處理等工具箱為數(shù)字濾波研究的蓬勃發(fā)展提供了有力的工具。本文介紹了一種基于MATLAB環(huán)境下對數(shù)字理濾波器進行設(shè)計與仿真的方法。在基于MATLAB環(huán)境的數(shù)字濾波器的設(shè)計過程中，MATLAB工具箱提供了幾種模擬濾波的原型產(chǎn)生函數(shù)—貝塞爾低通模擬濾波器原型，巴特沃斯濾波器原型，切比雪夫（Ⅰ型、Ⅱ型）濾波器原型，橢圓濾波器原型等不同的模擬濾波器原型；模擬低通濾波器原型向低通、高通、帶通、帶阻的轉(zhuǎn)變函數(shù)；從模擬濾波器向數(shù)字濾波器轉(zhuǎn)化的雙線性變換和沖激響應(yīng)不變法；模擬數(shù)字IIR濾波器階數(shù)選擇函數(shù)以及數(shù)字濾波器直接設(shè)計函數(shù)等。這一整套設(shè)計函數(shù)給在MATLAB中設(shè)計IIR數(shù)字帶來了極大的方便。                                

目錄

1.1數(shù)字濾波器概述……………………………………1

1.2 MATLAB概述………………………………………3

2.1 IIR濾波器設(shè)計的常用方法………………………5

2.2雙線性變換法設(shè)計IIR數(shù)字濾波器………………9

2.3 脈沖響應(yīng)不變法……………………………………14

2.4 完全濾波器的設(shè)計…………………………………18

數(shù)字濾波器及MATLAB語言概述

1.1數(shù)字濾波器概述

1.1.1數(shù)字濾波器的定義

數(shù)字濾波器是指完成信號濾波處理功能的，用有限精度算法實現(xiàn)的離散時間線性非時變系統(tǒng)，其輸入是一組數(shù)字量，其輸出是經(jīng)過變換的另一組數(shù)字量。因此，數(shù)字濾波器本身既可以是用數(shù)字硬件裝配成的一臺完成給定運算的專用的數(shù)字計算機，也可以將所需要的運算編成程序，讓通用計算機來執(zhí)行。數(shù)字濾波器，輸入輸出均為數(shù)字信號，通過一定的運算關(guān)系，改變輸入信號中所含頻率成分的相對比例，或則濾除某些頻率成分的器件。

對于數(shù)字濾波器而言，若系統(tǒng)函數(shù)為H(z),其脈沖響應(yīng)為h(n),輸入時間序列為x(n),則它們在時域內(nèi)的關(guān)系式如下：

y(n)=h(n)﹡x(n)                       （1-1）

在Z域內(nèi)，輸入和輸出存在如下關(guān)系：

Y(z)= H(z)X(z)                       （1-2）

式中，X(z)、Y(z)分別為x(n)和y(n)的Z變換。

在頻域內(nèi)，輸入和輸出則存在如下關(guān)系：

Y(j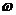)=H(j)X(j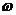)                   （1-3）

式中，H(j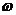)是數(shù)字濾波器的頻率特性；X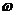(j)Y(j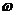)分別為x(n)和y(n)的頻譜，而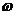為數(shù)字角頻率。

1.1.2數(shù)字濾波器的分類

數(shù)字濾波器可以有很多種分類方法，但總體上可分為兩大類。一類稱為經(jīng)典濾波器，即一般的濾波器，其特點是輸入信號中的有用成分和希望濾除的成分占用不同的頻帶，通過合適的選頻濾波器可以實現(xiàn)濾波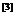。例如，若輸入信號中有干擾，信號和干擾的頻帶互不重疊，則可濾出信號中的干擾得到純信號。但是，如果輸入信號中信號和干擾的頻帶相重疊，則干擾就不能被有效的濾出。另一類稱為現(xiàn)代濾波器，如維納濾波器、卡爾曼濾波器等，其輸入信號中有用信號和希望濾除的成分頻帶重疊。對于經(jīng)典濾波器，從頻域上也可以分為低通、高通、帶通和帶阻濾波器。從時域特性上看，數(shù)字濾波器還可以分為有限沖激響應(yīng)數(shù)字濾波器（FIR）和無限沖激響應(yīng)數(shù)字濾波器（IIR）。

對于有限沖激響應(yīng)數(shù)字濾波器（FIR），其輸出y(n)只取決于有限個過去和現(xiàn)在的輸入，x(n),x(n-1),…,x(n-m),濾波器的輸入輸出關(guān)系可表示為

y(n)=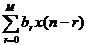                    （1-4）

對于無限沖激響應(yīng)數(shù)字濾波器（IIR），它的輸出不僅取決于過去和現(xiàn)在的輸入，而且還取決于過去的輸出，其差分方程為

y(n)+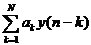= 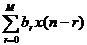          (1-5)

該差分方程的單位沖激響應(yīng)是無限延續(xù)的。

1.1.3常用濾波器的性能指標

濾波器性能一般用系統(tǒng)頻率特性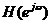來說明，常用的性能指標主有以下三個參數(shù)：

1. 幅度平方函數(shù)

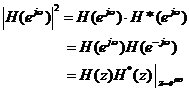                   (1-6)

該性能指標主要用來說明系統(tǒng)的幅頻特性。

2. 相位函數(shù)

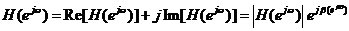        (1-7)

其中：

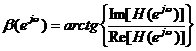                  (1-8)

該指標主要用來說明系統(tǒng)的相位特性。

3. 群延時

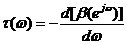                        （1-9）

定義為相位對角頻率導(dǎo)數(shù)的負值，說明了濾波器對不同的頻率成分的平均延時。當(dāng)要求在通帶內(nèi)的群延遲是常數(shù)時，濾波器相位響應(yīng)特性是線性的。

它以矩陣運算為基礎(chǔ)，把計算、可視化、仿真設(shè)計融合到一個交互式的工作環(huán)境中。尤其是MATLAB工具箱使各個領(lǐng)域的研究人員可以直觀方便地進行科學(xué)研究和工程應(yīng)用。其中的信號處理、圖像處理等工具箱為數(shù)字濾波研究的蓬勃發(fā)展提供了有力的工具。

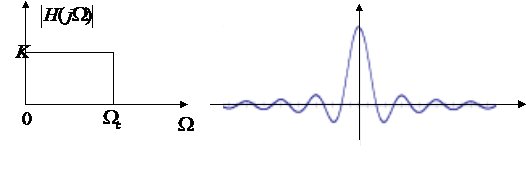
實際設(shè)計中所能得到的濾波器的頻率特性與理想濾波器的頻率特性之間存在著一些顯著的差別，現(xiàn)以低通濾波器的頻率特性為例進行說明。

1.理想低通濾波器的特性：

設(shè)濾波器輸入信號為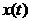，信號中混入噪音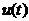，它們有不同的頻率成分。濾波器的單位脈沖響應(yīng)為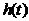。則理想濾波器輸出為：

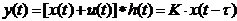             （1-10）

即噪音信號被濾除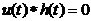，而信號無失真只有延時和線性放大。對上式作傅里葉變換得：

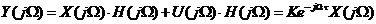  （1-11）

假定噪音信號被濾除，即：

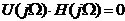                 （1-12）

整理得：

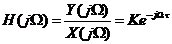              （1-13）

圖1-1 理想低通濾波器頻率特性       圖1-2 理想濾波器的單位脈沖響應(yīng)

假定信號頻率成分為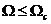：，噪音頻率成分為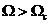。則完成濾波的理想低通濾波器特性是：

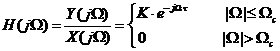       (1-14)

即：

                (1-15)

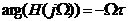                    (1-16)

系統(tǒng)的單位脈沖響應(yīng)為：

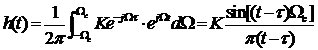       (1-17)

理想低通濾波器的頻率特性如圖1-1所示，單位脈沖響應(yīng)的波形如圖1-2所示。

理想濾波器具有非因果、無限長的單位脈沖響應(yīng)和不連續(xù)的頻率特性，要用穩(wěn)定的線性時不變（LTI）系統(tǒng)來實現(xiàn)這樣的特性是不可能的。工程上是用脈沖響應(yīng)為有限長的、因果的、穩(wěn)定的線性時不變系統(tǒng)或具有連續(xù)頻率特性的線性時不變系統(tǒng)來逼近理想特性。在滿足一定的誤差要求的情況下來實現(xiàn)理想濾波特性。因此實際的濾波器的頻率特性如圖1-3所示。

其中：

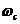——截止頻率

——阻帶起始頻率

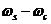——過渡帶寬

在通帶內(nèi)幅度響應(yīng)以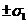的誤差接近于1，即：

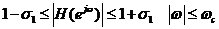             (1-18)

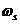為阻帶起始頻率，在阻帶內(nèi)幅度響應(yīng)以小于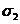的誤差接近于零，即：

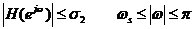               (1-19)

為了使逼近理想低通濾波器的方法成為可能，還必須提供一帶寬為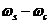的不為零的過渡帶。在這個頻帶內(nèi)，幅度響應(yīng)從通帶平滑的下落到阻帶。

1.2 MATLAB概述

MATLAB是美國MathWorks公司開發(fā)的一種功能極其強大的高技術(shù)計算語言和內(nèi)容極其豐富的軟件庫，集數(shù)值計算、矩陣運算和信號處理與顯示于一身。該軟件最初是由美國教授Cleve Moler創(chuàng)立的。1980年前后，他在教線性代數(shù)課程時，發(fā)現(xiàn)用其他高級語言編程時極不方便，便構(gòu)思開發(fā)了MATLAB，即矩陣實驗室（Matrix Laboratory）。該軟件利用了當(dāng)時代表數(shù)值線性代數(shù)領(lǐng)域最高水平的EISPACK和LINPACK兩大軟件包，并且利用Fortran語言編寫了最初的一套交互式軟件系統(tǒng)，MATLAB的最初版本便由此產(chǎn)生了。      

最初的MATLAB由于語言單一，只能進行矩陣的運算，繪圖也只能用原始的描點法，內(nèi)部函數(shù)只有幾十個，因此功能十分簡單。1984年該公司推出了第一個MATLAB的商業(yè)版，并用C語言作出了全部改寫。現(xiàn)在的MATLAB程序是MathWorks公司用C語言開發(fā)的，第一版由steve Bangert主持開發(fā)編譯解釋程序，Steve Kleiman完成圖形功能的設(shè)計，John Little和Cleve Moler主持開發(fā)了各類數(shù)學(xué)分分析的子模塊，撰寫用戶指南和大部分的M文件。接著又添加了豐富的圖形圖像處理、多媒體功能、符號運算和與其它流行軟件的接口功能，使MATLAB的功能越來越強大。

MTALAB系統(tǒng)主要由以下五個部分組成：

(1)MATALB語言體系。 MATLAB是高層次的矩陣／數(shù)組語言，具有條件控制、函數(shù)調(diào)用、數(shù)據(jù)結(jié)構(gòu)、輸入輸出、面向?qū)ο蟮瘸绦蛘Z言特性。利用它既可以進行小規(guī)模端程，完成算法設(shè)計和算法實驗的基本任務(wù)，也可以進行大規(guī)模編程，開發(fā)復(fù)雜的應(yīng)用程序。

(2)MATLAB工作環(huán)境 。這是對MATLAB提供給用戶使用的管理功能的總稱。包括管理工作空間中的變量據(jù)輸入輸出的方式和方法，以及開發(fā)、調(diào)試、管理M文件的各種工具。

(3)圖形句相系統(tǒng) 。這是MATLAB圖形系統(tǒng)的基礎(chǔ)，包括完成2D和3D數(shù)據(jù)圖示、圖像處理、動畫生成、圖形顯示等功能的高層MATLAB命令，也包括用戶對圖形圖像等對象進行特性控制的低層MATLAB命令，以及開發(fā)GUI應(yīng)用程序的各種工具。

(4)MATLAB數(shù)學(xué)函數(shù)庫。這是對MATLAB使用的各種數(shù)學(xué)算法的總稱。包括各種初等函數(shù)的算法，也包括矩陣運算、矩陣分析等高層次數(shù)學(xué)算法。

(5)MATLAB應(yīng)用程序接口(API)。這是MATLAB為用戶提供的一個函數(shù)庫，使得用戶能夠在MATLAB環(huán)境中使用C程序或FORTRAN程序，包括從MATLAB中調(diào)用于程序(動態(tài)鏈接)，讀寫MAT文件的功能。

除此之外，MATLAB系統(tǒng)還具有如下特點：

（1）具有易學(xué)易用的語言體系；

（2）具有交互式的工作環(huán)境；

（3）具有多層面的圖像處理系統(tǒng)；

（4）具有豐富高效的MATLAB工具箱；

（5）具有便利的程序接口（API）;

（6）應(yīng)用領(lǐng)域廣泛；

（7）嵌入了面向?qū)ο缶幊陶Z言。

濾波器的設(shè)計

2.1 IIR濾波器設(shè)計的常用方法

IIR數(shù)字濾波器的系統(tǒng)函數(shù)為：

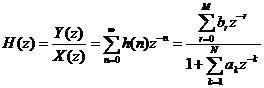       （2-1）

IIR濾波器設(shè)計就是根據(jù)性能指標要求，設(shè)計濾波器的分子和分母多項式。IIR數(shù)字濾波器的設(shè)計通常借助于模擬濾波器原型，再將模擬濾波器轉(zhuǎn)換為數(shù)字濾波器。模擬濾波器的理論和設(shè)計方法已發(fā)展得相當(dāng)成熟，且有一些典型的模擬濾波器供我們選擇，如巴特沃斯(Butterworth)濾波器、切比雪夫(Chebyshev)濾波器、橢圓(Cauer)濾波器、貝塞爾(Bessel)濾波器等，這些典型的濾波器各有特點。本文采用經(jīng)典設(shè)計法中的模擬濾波器變換法和完全設(shè)計函數(shù)法分別來設(shè)計數(shù)字濾波器。

用MATLAB進行典型的數(shù)字濾波器的設(shè)計，一般步驟如下:

(1)按一定規(guī)則將給出的數(shù)字濾波器的技術(shù)指標轉(zhuǎn)換成模擬低通濾波器的技術(shù)指標;

(2)根據(jù)轉(zhuǎn)換后的技術(shù)指標使用濾波器階數(shù)選擇函數(shù)，確定最小階數(shù)N和固有頻率Wn，根據(jù)選用的模擬低通濾波器的類型可分別用函數(shù):buttord、cheb1ord、cheb2ord、ellipord等;

(3)運用最小階數(shù)N產(chǎn)生模擬濾波器原型，模擬低通濾波器的創(chuàng)建函數(shù)有:buttap、cheb1ap、cheb2ap、ellipap等;

(4)運用固有頻率Wn把模擬低通濾波器原型轉(zhuǎn)換成模擬低通、高通、帶通、帶阻濾波器，可分別用函數(shù)lp2lp、lp2hp、lp2bp、lp2bs;

(5)運用沖激響應(yīng)不變法或雙線性變換法把模擬濾波器轉(zhuǎn)換成數(shù)字濾波器，分別用函數(shù)impinvar和bilinear來實現(xiàn)。

2.2雙線性變換法設(shè)計IIR數(shù)字濾波器

在MATLAB中，雙線性變換法的調(diào)用函數(shù)是bilinear。其調(diào)用格式為：

a. [zd,pd,kd]= bilinear(z,p,k,fs)

b. [zd,pd,kd]= bilinear(z,p,k,fs,fp)

c. [numd,dend]=bilinear(num,den,fs)

d. [numd,dend]=bilinear(num,den,fs,fp)

e. [Aa,Bb,Cc,Dd]=bilinear(A,B,C,D,fs)

f. [Aa,Bb,Cc,Dd]=bilinear(A,B,C,D,fs,fp)

[zd,pd,kd]=bilinear(z,p,k,fs)是把模擬濾波器的零極點模型轉(zhuǎn)換為數(shù)字濾波器的零極點模型，fs為采樣頻率，z,p,k分別為濾波器的零點、極點和增益；

[numd,dend]=bilinear(num,den,fs)是把模擬濾波器的傳遞函數(shù)模型轉(zhuǎn)換為數(shù)字濾波器的傳遞模型；

[Aa,Bb,Cc,Dd]=bilinear(A,B,C,D,fs)是把模擬濾波器的狀態(tài)方程模型轉(zhuǎn)換為數(shù)字濾波器狀態(tài)方程模型。

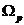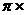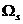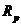例如，用雙線性變換法設(shè)計一個巴特沃思數(shù)字低通濾波器，技術(shù)指標如下：通帶截止頻率=24k rad/s，阻帶截止頻率=28k rad/s，通帶波紋系數(shù)=0.3dB, 阻帶波紋系數(shù)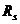=50dB,采樣頻率fs=20000Hz。

程序如下：

[N,Wn]=buttord(wp,ws,Rp,Rs,’s’)    %估計濾波器最小階數(shù)

[z,p,k]=buttap(N);

[Bap,Aap]=zp2tf(z,p,k);

[b,a]=lp2lp(Bap,Aap,Wn);

[bz,az]=bilinear(b,a,fs)

freqz(bz,az,Nn,fs)

程序在MATLAB環(huán)境下的運行及結(jié)果如圖2-1所示：

結(jié)果如下：

N =11

Wn =1.4892e+004

bz =

  Columns 1 through 6

    0.0110    0.1211    0.6055    1.8166    3.6333    5.0866

  Columns 7 through 12

    5.0866    3.6333    1.8166    0.6055    0.1211    0.0110

az =

  Columns 1 through 6

1.0000    2.7098    4.6379    5.2252    4.3685    2.7207

  Columns 7 through 12

1.2885    0.4561    0.1181    0.0211    0.0023    0.0001

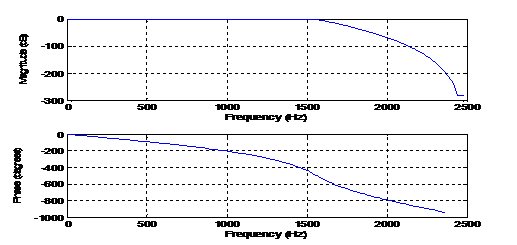
圖2-1  巴特沃思數(shù)字低通濾波器幅頻-相頻特性

2.3 脈沖響應(yīng)不變法

脈沖響應(yīng)不變法就是要求數(shù)字濾波器的脈沖響應(yīng)序列h(n)與模擬濾波器的脈沖響應(yīng)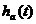的采樣值相等，即

h(n)=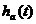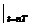= 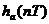          （2-2）            

式中，T為采樣周期。根據(jù)模擬信號的拉普拉斯變換與離散序列的Z變換之間的關(guān)系，我們知道

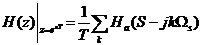                （2-3）                                 

此式表明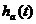，的拉普拉斯變換在s平面上沿虛軸，按照周期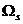=2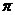/T延拓后，按式z=，進行Z變換，就可以將Ha(s)映射為H(z)。事實上，用脈沖響應(yīng)不變法設(shè)計IIR濾波器，只適合于Ha(s)有單階極點,且分母多項式的階次高于分子多項式階次的情況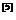。將Ha(s)用部分分式表示：     

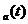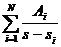
Ha(s)=LT[h]=         （2-4）           

式中，LT[·]代表拉普拉斯變換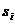，為的單階極點。將Ha(s)進行拉普拉斯反變換，即可得到

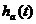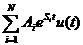=                 （2-5）   

式中，u(t)是單位階躍函數(shù)。則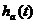的離散序列（對它進行抽樣）：h(n)=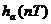= 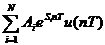            （2-6）

對h(n)進行z變換之后，可以得到數(shù)字濾波器的系統(tǒng)函數(shù)H(z)

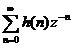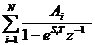
H(z)==         （2-7）  

對比Ha(s)與H(z)，我們會發(fā)現(xiàn)：s域中Ha(s)的極點是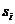，映射到z平面之后，其極點變成了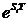，而系數(shù)沒有發(fā)生變化，仍為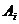。因此，在設(shè)計IIR濾波器時，我們只要找出模擬濾波器系統(tǒng)函數(shù)Ha(s)的極點和系數(shù)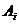，通過脈沖響應(yīng)不變法，代入H(z)的表達式中，即可求出H(z)，實現(xiàn)連續(xù)系統(tǒng)的離散化。

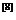但是脈沖響應(yīng)不變法只適合于設(shè)計低通和帶通濾波器，而不適合于設(shè)計高通和帶阻濾波器。因為，如果模擬信號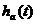的頻帶不是介于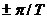之間，則會在的奇數(shù)倍附近產(chǎn)生頻率混疊現(xiàn)象，映射到z平面后，則會在附近產(chǎn)生頻率混疊現(xiàn)象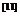。從而使所設(shè)計的數(shù)字濾波器不同程度的偏離模擬濾波器在附近的頻率特性，嚴重時使數(shù)字濾波器不滿足給定的技術(shù)指標。為此，希望設(shè)計的濾波器是帶限濾波器，如果不是帶限的，例如，高通濾波器、帶阻濾波器，需要在高通濾波器、帶阻濾波器之前加保護濾波器，濾出高于折疊頻率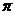/T以上的頻帶，以免產(chǎn)生頻率混疊現(xiàn)象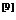。但這樣會增加系統(tǒng)的成本和復(fù)雜性。因此，高通與帶阻濾波器不適合用這種方法。

在MATLAB中，脈沖響應(yīng)不變法的調(diào)用函數(shù)是impinvar，其調(diào)用格式為：

a. [bz,az]=impinvar(b,a,fs)

b. [bz,az]=impinvar(b,a)

c. [bz,az]=impinvar(b,a,fs,tol)

該函數(shù)的功能是將分子向量為b、分母向量為a的模擬濾波器，轉(zhuǎn)換為分子向量為bz、分母向量為az的數(shù)字濾波器。fs為采樣頻率，單位為Hz，默認值為1Hz。tol指誤差容限，表示轉(zhuǎn)換后的離散系統(tǒng)函數(shù)是否有重復(fù)的極點。

例如，用脈沖響應(yīng)不變法設(shè)計一個契比雪夫1型數(shù)字低通濾波器，指標要求：通帶截止頻率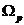=1000Hz，阻帶截止頻率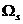=1200Hz，采樣頻率fs=5000Hz，通帶衰減系數(shù)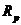=0.3dB，阻帶衰減系數(shù)=40dB。

程序如下：

wp=1000*2*pi;ws=1200*2*pi;fs=2500;Rp=0.3;Rs=40;

[N,Wn]=cheb1ord(wp,ws,Rp,Rs,'s'); %估計濾波器最小階數(shù)

[z,p,k]=cheb1ap(N,Rp);            %模擬濾波器函數(shù)引用

[A,B,C,D]=zp2ss(z,p,k);           %返回狀態(tài)轉(zhuǎn)移矩陣形式

[AT,BT,CT,DT]=lp2lp(A,B,C,D,Wn); %頻率轉(zhuǎn)換

[b,a]=ss2tf(AT,BT,CT,DT);         %返回傳遞函數(shù)形式

[bz,az]=impinvar(b,a,fs);           %調(diào)用脈沖相應(yīng)不變法

[H,W]=freqz(bz,az);               %返回頻率響應(yīng)

plot(W*fs/(2*pi),abs(H));           %畫圖

grid;

xlabel('frequency/Hz');         

ylabel('magnitude');

N,Wn

N =11  Wn =6.2832e+003

程序在MATLAB環(huán)境下的運行及結(jié)果如圖2-2所示：

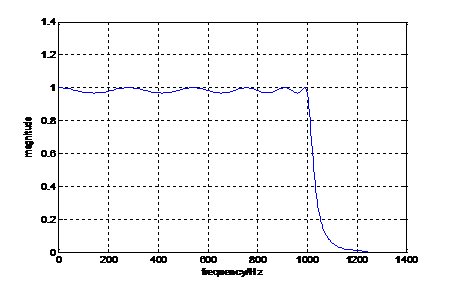
圖 2-2  契比雪夫型數(shù)字低通濾波器幅頻特性曲線

2.4 完全濾波器的設(shè)計

在MATLAB信號處理工具箱提供了幾個直接設(shè)計IIR數(shù)字濾波器的函數(shù)，所用到的函數(shù)有butter、cheby1、cheb2ord、ellipd以及besself等。Butter用來直接設(shè)計巴特沃思數(shù)字濾波器，cheby1用來直接設(shè)計切比雪夫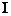型濾波器，cheb2ord用來設(shè)計切比雪夫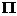型濾波器，ellipd用來設(shè)計橢圓濾波器，besself用來設(shè)計貝塞爾濾波器。完全濾波器的設(shè)計就是根據(jù)設(shè)計要求，直接調(diào)用函數(shù)來設(shè)計所需要的數(shù)字濾波器。主要函數(shù)的特點如下：

1、設(shè)計Butterworth濾波器用函數(shù)butter()，可以設(shè)計低通、高通、帶通和帶阻的數(shù)字和模擬濾波器，其特性是通帶內(nèi)的幅度響應(yīng)最大限度的平滑，但損失了截止頻率處的下降斜度。

2、設(shè)計Chebyshevl型濾波器用函數(shù)chebyl()。可以設(shè)計低通、高通、帶通和帶阻的數(shù)字和模擬Chebyshevl型濾波器，其通帶內(nèi)為等波紋，阻帶內(nèi)為單調(diào)。Chebyshevl型濾波器的下降斜度比II型大，但其代價是通帶內(nèi)波紋較大。

3、設(shè)計Chebyshev11型濾波器用函數(shù)cheby2()。可以設(shè)計低通、高通、帶通和帶阻的數(shù)字和模擬ChebyshevII型濾波器，其通帶內(nèi)為單調(diào)，阻帶內(nèi)等波紋。ChebyshevII型濾波器的下降斜度比I型小，但其阻帶內(nèi)波紋較大。

4、設(shè)計橢圓濾波器用函數(shù)ellip()，與chebyl、cheby2類似，可以設(shè)計低通、高通、帶通和帶阻的數(shù)字和模擬濾波器。與Butterworth和Chebyshev濾波器相比，ellip函數(shù)可以得到下降斜度更大的濾波器，得通帶和阻帶均為等波紋。一般情況下，橢圓濾波器能以最低的階實現(xiàn)指定的性能指標。

以上幾種函數(shù)在低通濾波器設(shè)計中的比較：

設(shè):Wp=30Hz，Ws=35Hz，F(xiàn)s=100，Rp=0.sdB，Rs=4odB分別用巴特沃斯(Butterworth)濾波器、切比雪夫(chebyshev)濾波器、橢圓(Cauer)濾波器，程序設(shè)計如下:

巴特沃斯低通濾波器:

[nl，Wnl]=buttord(wp/(Fs/2)，ws/(Fs/2)，rp，rs，’z’);

[numl，denl]=butter(nl，Wnl);

切比雪夫I型低通濾波器:

[n2，Wn2]=cheb1ord(wp/(Fs/2)，ws/(Fs/2)，rp，rs，’z’):

[num2，den2]=ehebyl(n2，rp，Wn2);

切比雪夫II型低通濾波器:

[n3，Wn3]=ehebZord(wp/(Fs/2)，ws/(Fs/2)，rp，rs，’z’);

[num3，den3]=cheby2(n3，rp，Wn3):

橢圓低通濾波器:

[n4，Wn4]=ellipord(wp/(Fs/2)，ws/(Fs/2)，rp，rs，’z’):

[num4，den4]=ellip(n3，rp，rs，Wn3);