第一章 緒論1.1引言
最小拍控制是一種直接數字設計方法。所謂最小拍控制就是要求閉環系統對于某種特定的輸入在最少個采樣周期內達到無靜差的穩態是系統輸出值盡快地跟蹤期望值的變化,因此最小拍實際上是時間最優控制。
近年來,隨著工業控制技術和航空航天技術的高速發展,人們對控制器的要求也越來越高。一般控制器具有以下要求:
- 精確性:指的是對特定輸入的系統,到達穩態后,系統輸出的采樣值能準確跟蹤輸入信號,也就是說采樣點上的輸出不存在穩態誤差。
- 快速性:系統能在有限的拍數下達到穩態的設計狀態嗎也就是系統準確的跟蹤輸入量縮需的采樣周期應為最少。
- 穩態性:控制器必須在物理上可實現且應該是穩定的閉環系統。
最小拍控制是一種直接數字設計方法。所謂最小拍控制就是要求閉環系統對于某種特定的輸入在最少個采樣周期內達到無靜差的穩態使系統輸出值盡快地跟蹤期望值的變化。因此最小拍控制實際上是時間最優控制。
在數字隨動控制系統中,要求系統的輸出值盡快地跟蹤給定值的變化,最控制就是為滿足這一要求的一種離散化設計方法。所謂的最小拍控制,就是要求閉環系統對于某種特定的輸入在最少個采樣周期內達到無靜差的穩態,且閉環脈沖傳遞函數有以下形式:
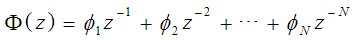
式中,N是可能情況下的最小正整數。這一形式表明閉環系統的脈沖響應在N個采樣周期后變為零,從而意味著系統在N拍之內達到穩態。但是最小拍控制器有其局限性:1、最小拍控制器對典型輸入的適應性較差。一種典型的最小拍閉環脈沖傳遞函數 2、最小拍控制器的可實現性問題。對于某些對象的脈沖傳遞函數,所設計的閉環脈沖傳遞函數,系統的響應超前于被控對象的輸入,這在實際中是實現不了的。3、最小拍控制的穩定性問題。在選擇時必須有一個約束條件的零點和不穩定極點能夠完全對消。
1.2設計任務要求
采用零階保持器的單位反饋離散系統,被控對象為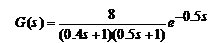 ,如下圖所示,其中
,如下圖所示,其中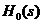 為零階保持器,
為零階保持器,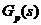 為被控對象,
為被控對象,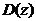 即為待設計的最少拍控制器。設計實現最小拍控制的simulink仿真模型,要求按照單位階躍輸入和單位速度輸入設計最小拍控制器,觀察其輸出曲線,整定參數后,系統階躍響應超調<10%并且分析最小拍控制器設計的特點。
即為待設計的最少拍控制器。設計實現最小拍控制的simulink仿真模型,要求按照單位階躍輸入和單位速度輸入設計最小拍控制器,觀察其輸出曲線,整定參數后,系統階躍響應超調<10%并且分析最小拍控制器設計的特點。

最少拍系統框圖
1.3設計技術參考數據
- 采樣周期T設置為1s。
- 零階保持器
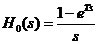 。
。 - 本文所指最少拍系統設計,是指系統在典型輸入信號(如階躍信號,速度信號,加速度信號等)作用下,經過最少拍(有限拍),使系統輸出的穩態誤差為零。
- 廣義被控對象的脈沖傳遞函數在z平面單位圓上及單位圓外沒有極點,且不含有純滯后環節。
1.4應完成的技術文件
第二章 課程設計說明書2.1綜述
在采樣系統中,時間經過一個采樣周期稱為一拍。最少拍系統設計,是指系統在典型輸入信號(如階躍信號,速度信號,加速度信號等)作用下,經過最少拍(有限拍),使系統輸出的穩態誤差為零。所以,最少拍控制系統的性能指標包括系統穩定、在典型輸入下穩態誤差為零、系統的調節時間最短或盡可能短,即最少拍系統對閉環脈沖傳遞函數的要求是穩定、準確和快速。本課程設計針對穩定、不含純滯后環節的被控對象,來推導數字控制器D(z)具有的形式。
2.2 被控對象穩定且不包含純滯后環節的最少拍控制器設計
控制系統結構如圖1所示,其中H0(s)為零階保持器,GP(s)為被控對象,D(z)即為待設計的最少拍控制器。
圖1 最少拍隨動系統框圖

定義廣義被控對象的脈沖傳遞函數為
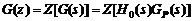
廣義被控對象的脈沖傳遞函數在z平面單位圓上及單位圓外沒有極點,且不含有純滯后環節。
閉環脈沖傳遞函數為
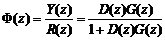 (1)
(1)
誤差脈沖傳遞函數
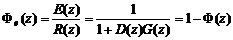 (2)
(2)
數字控制器
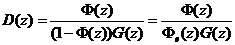 (3)
(3)
根據式(2)知
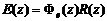 (4)
(4)
將其展開成如下形式:
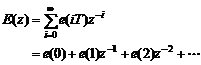 (5)
(5)
由式(6.4)可知,E(z)與系統結構Φe(z)及輸入信號R(z)有關。由式(5)可以看出,根據最少拍控制器的快速性設計準則,系統輸出應在有限拍N拍內和系統輸入一致,即i≥N之后,e(i)=0,也就是說,E(z)只有有限項。因此,在不同輸入信號R(z)作用下,根據使E(z)項數最少的原則,選擇合適的Φe(z),即可設計出最少拍無靜差系統控制器。
常見的典型輸入信號有:
單位階躍輸入 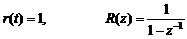
單位速度輸入 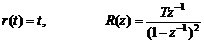
單位加速度輸入 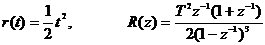
……
一般地,典型輸入信號的z變換具有如下形式:
 (6)
(6)
式中,A(z-1)是不包含(1-z-1)因式的z-1的多項式。
將式(6)代入式(4),得到
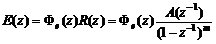 (7)
(7)
因此,從準確性要求來看,為使系統對式(6.6)的典型輸入信號無穩態誤差,Φe(z)應具有的一般形式為:
 (8)
(8)
式中,F(z-1)是不含(1-z-1)因式的z-1的有限多項式。根據最少拍控制器的設計原則,要使E(z)中關于z-1的項數最少,應該選擇合適的Φe(z),即選擇合適的p及F(z-1) ,一般取F(z-1)=1,p=m。式(8)及式(3)是設計最少拍控制系統的一般公式。
在不同典型輸入下,數字控制器的形式不同。
(1) 單位階躍輸入r(t)=1(t)
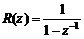
為使E(z)項數最少,選擇p=1,F(z-1)=1,即Φe(z)=1-z-1,則
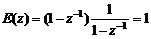
由z變換定義可知e(t)為單位脈沖函數,即
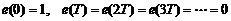
也就是說,系統經過1拍,輸出就可以無靜差地跟蹤上輸入信號,此時系統的調節時間ts=T,T為系統采樣時間。
(2) 單位速度輸入r(t)=t
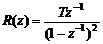
由式(8)易知,選擇p=2, F(z-1)=1, 即Φe(z)=(1-z-1)2,則:

則e(0)=0,e(T)=T,e(2T)=e(3T)=e(4T)=…=0,即系統經過2拍,輸出無靜差地跟蹤上輸入信號,系統的調節時間ts=2T。
(3) 單位加速度輸入r(t)=t2/2
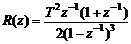
由式(7)可知,選擇p=3,F(z-1)=1,即φe(z)=(1-z-1)3,可使E(z)有最簡形式:
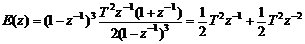
則e(0)=0, 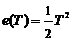 ,
, ,e(3T)=e(4T)=…=0,即經過3拍,系統的輸出可以無靜差地跟蹤上輸入,即系統調節時間ts=3T。
,e(3T)=e(4T)=…=0,即經過3拍,系統的輸出可以無靜差地跟蹤上輸入,即系統調節時間ts=3T。
由上面討論可以看出,在進行最少拍控制器設計時,誤差脈沖傳遞函數Φe(z)的選取與輸入信號的形式密切相關,對于不同的輸入信號r(t),所要求的誤差脈沖傳遞函數Φe(z)不同。所以這樣設計出的控制器對各種典型輸入信號的適應能力較差。若運行時的輸入信號與設計時的輸入信號形式不一致,將得不到期望的最佳性能。
表1 三種典型輸入信號形式下的最少拍控制器設計結果
第三章 方案分析及設計
3.1 廣義脈沖傳遞函數的求取
根據設計任務要求,設廣義被控對象的傳遞函數為
由Z變換,得
帶入
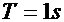
,得
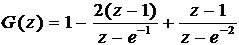
3.2最小拍控制器的設計
最小拍系統輸入信號形式不同,數字控制器也不同,根據表1三種典型輸入信號形式下的最少拍控制器設計結果,分別設計單位階躍輸入和單位速度輸入相應的最小拍控制器。
3.2.1單位階躍信號
當
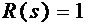
時,由Z變換得,
因此

數字控制器
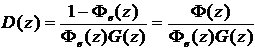
3.2.2單位速度信號
當
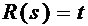
時,由Z變換得,
設
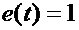
,則利用公式
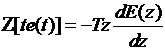
,得
因此

數字控制器
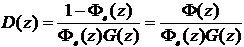
第四章 最小拍控制的simulink仿真模型4.1單位階躍信號的simulink仿真模型
4.2單位速度信號的simulink仿真模型
4.3仿真模型結果分析
當輸入信號為單位階躍信號時,按照最小拍控制策略設計的數字控制器,實現輸入經過一拍后,在采樣時刻系統穩態誤差為零,輸出跟蹤輸入但在采樣點間,系統輸出有紋波存在。
當輸入信號為單位速度信號時,按照最小拍控制策略設計的數字控制器,實現輸入經過兩拍后,在采樣時刻系統穩態誤差為零,輸出跟蹤輸入,但在采樣點間,系統輸出有紋波存在。
綜上所述,被控對象穩定且不包含純滯后環節,按最少拍原則設計數字控制器,雖然設計方法直觀簡單,又便于在計算機上實現,但也存在著缺點。
①系統輸出在采樣點間存在紋波,最少拍設計是保證在采樣點上穩態誤差為零,而在采樣點之間系統輸出可能存在波動,其原因在于數字控制器的輸出

經過兩拍后不為零或為常值,而是出于振蕩收斂。
②系統適應性差,最少拍原則是根據某種典型輸入信號設計的,對其它輸入信號不一定是最少拍,甚至可能產生很大的超調和靜差。
③控制幅值的約束最少拍設計實質上是時間最優調節系統,在此過程中,對數字控制器的輸出沒有做任何約束,但實際上控所能提供的能量是有限,所以采用最少拍原則設計的計算機控制系統,由于被控對象存在飽和特性,系統響應輸出不一定滿足最少拍目的。
心得體會這次課程設計我掌握了許多知識,不同于以往的課程設計,《計算機控制》課設的包經過一星期的《計算機控制》課程設計,收獲了很多。通過這幾天的學習,確實含面相當的廣泛,包括對上課時的理論基礎的回顧還有對數學工具MADLAB的學習掌握及單片機的使用。是一次對前面所學習科目的綜合設計。 在這次課程設計中,我學到了很多設計數字控制系統的思想與方法,應用了計算機控制課程上學到的知識,還用到了自動控制原理、模擬電子技術中的相關知識,給我提供了一個將所學的課程聯系在一起,并應用于實踐的機會。
參考資料[1] 張艷兵.王忠慶,鮮 浩.計算機控制技術[M].北京:國防工業出版社,2006
[2] 胡壽松.自動控制原理胡(第五版)北京:科學出版社,2007
[3] 樓順天.基于MATLAB的系統分析與設計(第2版),2005
[4] 張養安、劉林章,MATLAB軟件在數據處理中的應用, 2005
完整論文下載(word格式 可編輯):
 最小拍控制系統2.doc
(185.5 KB, 下載次數: 14)
最小拍控制系統2.doc
(185.5 KB, 下載次數: 14)
2017-7-24 11:08 上傳
點擊文件名下載附件
下載積分: 黑幣 -5