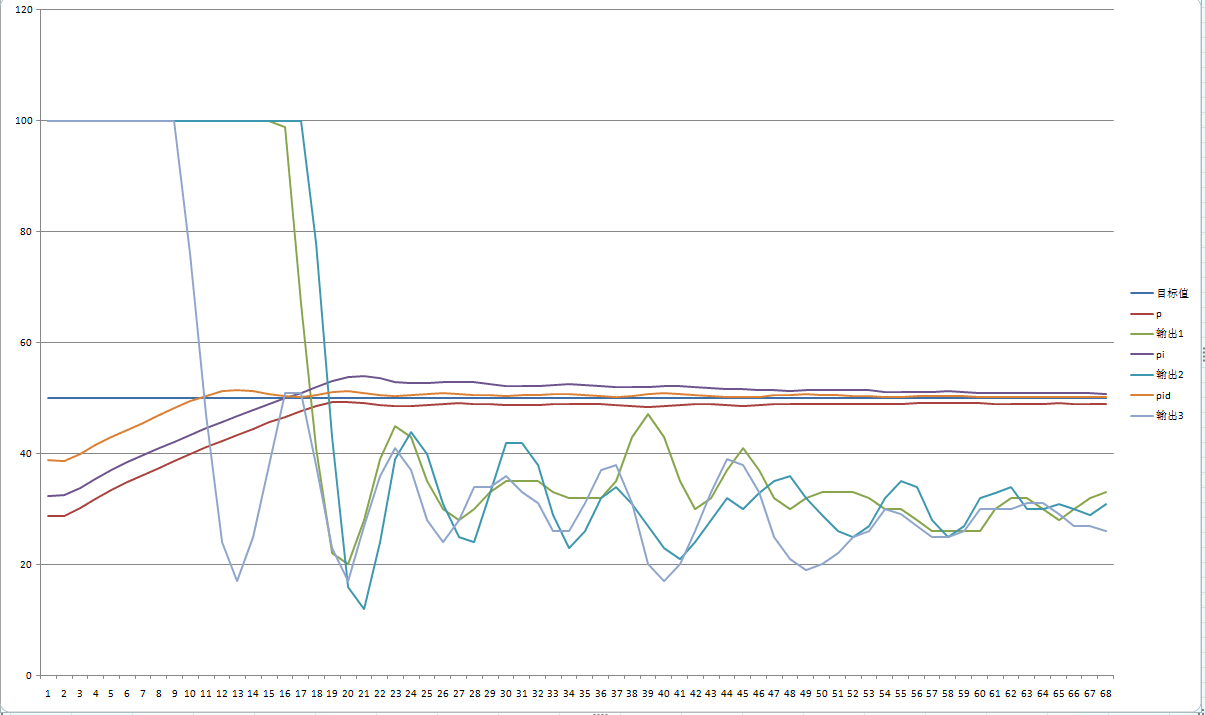
如上圖,無論是P還是PI控制都不可以使得和目標接近只有PID三個才可以使得它距離目標最近。
1、PID 簡介
PID = [ Kp*e(t)] + [Ki*∫(0-t)e(τ)dτ] + [Kd*de(t)/dt]
1.1、比例項
Pout = [ Kp*e(t)]
令x=e(t)則函數y=f(x)的形式f的取值為一個固定的數值,這樣在數軸上將會是一條固定斜率K的線。
他同步反映了自變量x的走向,f則成為走向的增益。也就是Kp,因為成線性成比例所以叫做比例項。
增益的大小決定了輸出的值的大小。增益大輸出值偏大,增益小輸出值偏小。
比例是誤差的對當前對當前進行影響結果就是曲線是震蕩的,系數越大震蕩的越劇烈。反之
1.2、積分項:
Iout =[Ki*∫(0-t)e(τ)dτ]
積分的概念好早就在學習,有過許多次的嘗試和請教,直到現在才逐漸的清晰起來,
必須從實際出發去著手理解,單純的看公式很難理解,因為畢竟我文化知識是個檻
首先我明確了積分是用來計算不規則曲線所包圍的面積的。
然后明確第二個概念是類似割圓術的,把她包圍的面積分解成小塊也就是所謂的dt
再有明確第三個概念就是極限的概念,早在數年前W生的高數書里面有看過lim->x,但是沒有明白是什么意思,事實上所謂的極限是無限接近而不等于的那個值。
積分里面就是相鄰的dt->0也就是說小到線變成了點,點和點的距離很小很小。這時候在兩點之的x,y坐標就是個矩形,就可以計算矩形的面積L*H然后一直加下去。
最后把所有的面積求和就得到了不規則曲線包圍的面積了。
之前請教過J和W 代數式的含義現在可以解釋上面的公式了,
∫(0-t)e(τ)dτ 0-t 表示X軸的時間坐標0-t這區間內,e(τ) 首先是 τ在區間0-t上,那么e(τ)就代表了在τ時間內的誤差值,散點定義在縱坐標上
這個e(τ)不一定是個線性,完全可能是個不規則的函數,然后dτ是對0-t之間的分成的份數,也就是dτ=t/lim->0,那么也就是在橫坐標的值,
他們之間的乘積就是那e(τ)*dt所包圍的一小塊的面積。前面的積分∫(0-t)我的理解可以等價于求和運算,將0-t區間內所有的e(τ)*dt小塊加起來,
那么他們的面積就應該是e(τ)在區間0-t之內的面積了。顯然她的值是隨著時間t增加而增加。數學上的dt->0在實際上是不可能的所以這就牽扯到dt的粒度,
dt粒度約小則e(τ)包圍的面積計算的約接近真實的值也大,反之粗略并值也相對小。事實上數學上的dt時間就是實際進行運算的頻率罷了。
最后一個就是Ki這個是積分的增益。顯然它越大則定積分所產生的值成倍數的增加,越小則積分值成倍的減小。
拋開Ki不看的話就是采樣計算時間內計算的面積之和,他需要時間去累計,輸出值看加入積分后結果增大,但是比純比例要穩定了。
積分是記錄了誤差的過去。會使的系統變得很穩定。但是還是會在目標值上下輕微的震蕩。
1.3、微分項:
Dout = [Kd*de(t)/dt]
微分的概念一直不理解,他們總是灌輸導數的概念,而我不能理解什么叫做導數。徹底的不理解。直到百度發現導數斜率,斜率我是知道的。
相應的微分的概念也要從實際出發。但是不像積分可以理解為不規則曲線的包圍面積,微分卻無法理解什么是需要微分的。
直到f的出現講到切線的概念。和直線的切線就是其本身。在加上之前的積分的dt概念所以得以繼續
任意一條不規則的線段,對其分割位無數份limx->0 ,那么又回到了和積分一樣的概念上每一份都變成了點,他們挨得很近。他們彼此的連線變成了規則的線。
宏觀上他們是不規則的線。微觀上他們點和點之間是規則的線。那么兩點之間的連線和X軸的夾角就是斜率了。
Kd就是微分增益控制,越大則微分值成倍提高,減小則微分值減小。對結果的影響小。
微分是對誤差未來走向,相當于有一定的提前量和預測性。會減小積分帶來的震蕩。使曲線輸出趨于平滑并等于設定值。
1.4、參數整定
參數整定就是對Kp\Ki\Kd進行配置。
第一種方法
調整比例其他參數=0
先對比例進行整定,逐漸的增加Kp并使得輸出曲線接近目標值,
此時關注開始的一個階段它的上升曲線比較陡,之后接著是震蕩,然后越來越小,后半部分呈現出紋波的形狀,
證明她正在震蕩,這種震蕩可以查看輸出驅動曲線可以明顯的顯現出來。我的整定是整定到離目標值約1-0.5左右。
此時再進行積分的整定保持比例不變的前提。開始增加積分值。此時發現曲線在開始的時候震蕩的很大,
超過比例的一大截。這是正常的,因為積分項的引入值變大了,輸出對應的變大了,這樣相當于開始的比例上抬了,所以震蕩會加劇,
調整的同時看后半部分的曲線是否接近目標,會發現真的很穩定并且在目標值以內0.5左右。偶爾會超過1,這時就應該停止整定
最后進行微分的整定。保持比例微分不變的前提條件,逐漸的增加微分值,然后使開始的比較的大的震蕩曲線減小到目標值左右,
比如以50為目標則原來在PI條件下峰值可以達到52,那么調整微分使她慢慢回落到50左右。不足達不到就慢慢的增加微分系數,直到達到之后。
停止所有的整定工作。保存KP KI KD的值。并寫入到PID中。
第二種方法
就是 齊格勒-尼克爾斯 整定。目前不用不做學習了。
1.5、微積分的時間dt
微積分的時間dt是微分和積分共同使用的粒度,它是X坐標的T時間,轉換為運算就是運算的頻率。單位是秒。這個需要根據對象的屬性進行調整。
溫度這種滯后的向大了調整,電機伺服這種要小才能跟上。 為系統選擇一個合適的微積分時間。給積分器和微分器提供計算基準是必須的。
1.6、輸出推動
按照0-100%輸出推動執行器件即可。做好上下限的窗口。沒有什么特殊要求的情況下是這樣。
by 老王
|