|
|
Δy
slope = -----
Δx 其中Δ表示某個變量的增量。比如說,
當x增加一小段,比如增加了2,此時y
也必然增加了一小段,比如1之類的,
那么增加的這一段的平均斜率就是:
Δy 1
slope = ----- = ---
Δx 2
這跟平均速度的計算 v=s/t 很像,
(事實上完全相同)
(注:對于一次函數 y = ax + b ,a就是它的斜率。 【注中注:這很明顯,因為如果x增加一段,比如增加了Δx, 那么Δy = a(x+Δx)+b-ax-b =ax+aΔx 斜率slope = Δy/Δx = a】 斜率的取值與b無關,因為之前說過,
速度的取值與起點無關。)
哦,這簡直像是在做代數運算,找不到微積分的影子。如果你前面的準備工作做好了,那么繼續請往下看,下面我將引入微分學最核心也是最有趣的部分。。
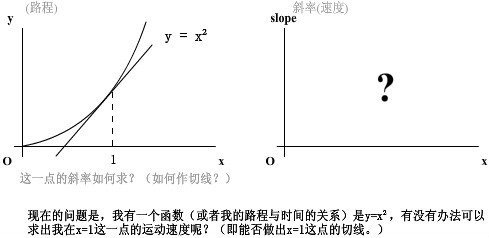
現在的問題是,我有一個函數(或者我的路程與時間的關系)是y=x,有沒有辦法可以
求出我在x=1這一點的運動速度呢?(即能否做出x=1這點的切線。)
“這一點的切線?天方夜譚!”你可能會發出這樣的感嘆。事實上一開始,數學家們碰到這樣的問題時也頭疼不已。但是他們找到了一種補救方法,就是:讓x=1增加Δx,求出這一段的平均斜率,用平均斜率來近似的代替這一點的斜率。增加之后的就是1+Δx,則
y的增加量為:
2
Δy = (1+Δx) - 1
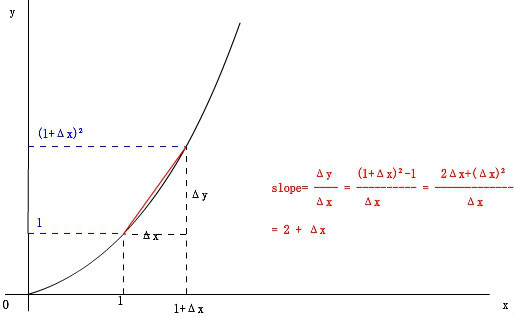
所以這一段(1, 1+Δx)的平均斜率就是:
2 2
Δy (1+Δx) - 1 2Δx + (Δx)
slope= ---- = ----------- = ------------
Δx Δx Δx
= 2 + Δx
我們知道,如果Δx越小,則得到的斜率越接近于這一點的真實斜率,而在上式中,我們發現如果讓Δx趨向于0,Δx就會消失!所以最終的結果很漂亮,這一點的斜率是2!
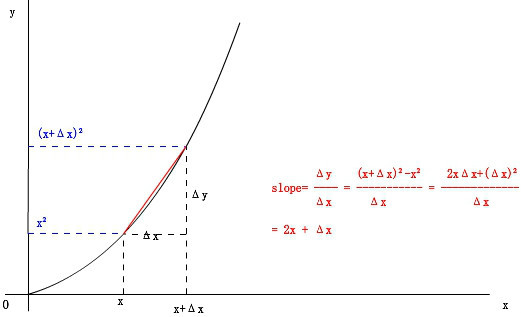
那么,對于任一點x ,函數y=x^2的斜率能求出嗎? 當然能!這種情況不過是上面的情況的推廣:
2 2 2
Δy (x+Δx) - x 2Δx + (Δx)
slope= ---- = ------------- = ---------------
Δx Δx Δx
= 2x + Δx
令Δx→0 (意思是讓Δx趨向于0),上式 = 2x 。即對于任意一點x,函數y=x^2的斜率是2x 。
那么一開始的問題我們就解決了:
(問題:)
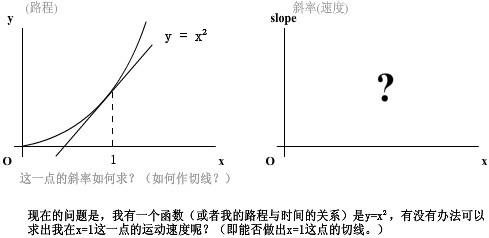
(解答:)
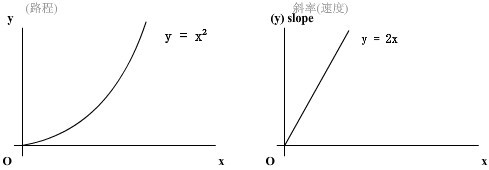
【解釋:函數y=x^2在x點的切線的斜率是2x。
(如果你的路程函數是x^2,你的速度函數就是2x。像這樣,知道路程函數,求得速度函數的過程就叫求導,這個“速度”函數就叫這個“路程”函數的導數 。
dy
函數y的導數記作 y' 或 ---- (讀作“d y d x”,不讀分數線。)。
dx
(即y=x^2,則y'=2x)
】
不管你信不信,你已經初步理解了微分學中的導數的概念!是不是很簡單?
【注:本文介紹的求導的過程實際上是不嚴謹的,因為導數的嚴格的定義是由極限給出的,而本篇沒有介紹極限,也沒有給出“連續”
的含義 】
下面寫出幾個常見的函數的導數,這些公式、求導法則可以直接用,沒必要每次都去推導一次。
常函數 的導數:
y = C y' = 0 (C為常數)
冪函數 的導數:
n n-1
y = x 則 y' = nx (n為常數)
【注:√x = x^0.5 ,根號也可以用這個求導法則,(√x)' = 1/(2√x) 】
例:y = x^2 + 2x + 3 ,求它的導數?
y'=2x + 2
例:y = 2x^100 ,求它的導數?
y'=2*100x^99 =200x^99
一般指數函數 的導數:
x x
y = a y' = a * ln a (a為常數)
指數函數 的導數:
x x
y = e y' = e
求導的加法法則:
(f + g)' = f' + g'
求導的乘法法則:
(f*g)' = f'g + f g'
求導的鏈式法則(重要!)
f[g(x)] ' = f'[g(x)]*g'(x)
【
解釋鏈式法則:
鏈式法則是用于遇到“復合函數”的求導時才用的,至于復合函數,是指一個函數“嵌套”在另一個函數里面。比如:
_____
y=√2x+1 ,是由根號函數y=√x 和線性函數y = 2x+1 "復合"而成的。對復合函數求導時,先對“外函數”求導,再把“內函數”的導數乘在外面。
比如 _____ _____ 1 y=√2x+1 ,外函數是√2x+1 ,內函數是2x+1,外函數的導數就是 --------- ,內函數的導數是2,因此這個復合函數的導數就是
_____
2√2x+1
1 1
y' = --------- × 2 = ----------
_____ ______
2√2x+1 √2x+1
】
(以上法則有些看不懂沒關系)
導數的用途
導數是微積分的重要概念和基礎。不過,你是否疑惑“導數除了做切線還能干什么用”,事實上導數非常有用而且其樂無窮,用途廣泛。這里僅舉2個簡單的例子說明(這只是導數應用的冰山一角):
1.物理應用:在物理里,如果一個物體的運動路程與時間的函數為s,則速度函數是s的導數。即 v = s'
2.函數應用:導數可以用來作切線,可以求出函數的 極大/極小值 點。因為函數的極大/極小值點上的切線的斜率為0,所以對于一個函數y,只要求出其導數y' ,其最大最小值一定在方程y'=0的解上。
例:求函數 y = x^3 - x^2 的極值?

易得其導數 y' = 3x^2 - 2x
令y' = 0 即 解方程 3x^2-2x = 0 解得 x = 0 或 x= 2/3
根據圖像可以看出x=0是極大值,x=2/3是極小值。
如果你知道“二階導數”這一概念,你可以用二階導數判斷極大值和極小值而無需畫圖。。而且極值點處二階導數不能為0,否則不是極值。當然,在不清楚二階導數時,你可以用作圖來輔助。
3.計算應用:(傳說中的線性近似)導數可以用來計算近似值。
10
例:計算 0.995
選取函數 y = x^10 ,發現x=0.995這一點跟x=1這一點很接近。我們作出其導數y' = 10x^9 ,
線性近似的概念就是用這一點x=1的切線去逼近x=0.995的值。
易知,x=1時y'=10,即這一點切線斜率為10, 這一點與x=0.995的差距是(1-0.995)=0.005,我們從x=1點開始,按照這一點的切線方向后退0.005,即Δx= -0.005,那么Δy=10 * -0.005 = -0.05,也就是說,按照切線方向,x下降了0.005,y也下降了0.05。
所以計算出的近似值就是 1 - 0.05 = 0.95
10
即 0.995 ≈ 0.95
如果你用計算器來檢驗,你會發現計算器的結果是 0.9511101305,和我們計算的結果非常接近。這就是微分(導數)在近似計算中的應用。
*例2:計算√2 的近似值 1
選取函數y = √x , y' = ------
2√x
我們知道,1.4^2=1.96,(即√1.96 = 1.4)。 1.96跟2很接近,所以我們就用x=1.96這一點的切線來近似x=2的值。
y'在1.96的取值y'(1.96) = 1/(2*1.4) ≈ 0.357,這是x=1.96這一點的切線。
現在讓x增加0.04,則y就會增加0.04*0.357 = 0.01428
所以√2 ≈ 1.4+0.1428 = 1.41428
如果你用計算器來檢驗,你會發現這樣做精確度還是很不錯的:√2 = 1.414213562 ,精確到了小數點后4位。
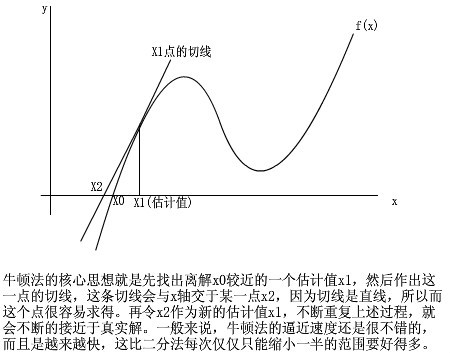
4.工程應用:導數可以解方程(詳細過程略,參見“牛頓法解方程”)
5.經濟學應用:經濟學中,導數稱為“邊際函數”,是一個重要而基礎的概念。
……
……等等等等……
有趣的問題,這也是微積分的實用之處:
R博士的家在A點。每天,R博士都要開著小汽車去他的公司C上班。他以前一直都是這樣走的:先從家垂直的開到B點,然后進入公路,再開到C點。其中AB=30km,CB=60km,R博士的汽車在公路CB上速度可以達到60km/h,但是在非公路地段只有30km/h。有一天R博士突發奇想,發現如果以某個角度開到某個P點進入公路,他所用的時間將大大縮短。不過現在R博士搞不清BP取多少時,他用的時間會最短。你能幫他確定這個BP的長度嗎?

如果設PB = x km,CP = 60-x
由勾股定理可得,AP= _________ √900 + x2
汽車在AP這段速度是30km/h,在CP這段速度是60km/h,所以可得R博士所需時間T與BP(x)的取值的函數關系: __________ √900 + x^2 60 - x T = ------------ + -------- 30 60
這不過是在求一個函數的極值。首先對它求導:
(注:這個2x↓是因為鏈式法則。內函數900 + x^2 的導數是2x,對復合函數求導時要乘在外面。現在不懂也沒有太大的關系)
2x 1
T' = ----------------- - ------
________ 60
30 * 2√900+x^2
令T' = 0,解方程:
2x 1 ----------------- = ------
________ 60
30 * 2√900+x^2
約分:
x 1 ----------------- = ------
________ 60
30 * √900+x^2
交叉相乘得 :
________
30√900+x^2 = 60x
兩邊約去30:
________ √900+x^2 = 2x
兩邊同平方:
900+x^2 = 4x^2
移項:
3x^2 = 900
約分:
x^2 = 300
直接開方法(舍去負根):
____ ______ __
x = √300 = √100*3 = 10√3 ≈ 17.32 km
所以,BP應取17.32 km。R博士應從這個P點進入公路。
【注:嚴格的數學中的導數被定義如下:
函數y=f(x)的導數dy/dx為:
dy Δy f(x+Δx) - f(x)
---- = lim ------ = lim ----------------
dx Δx→0 Δx Δx→0 Δx
在數學中,導數被定義為一個分式Δy/Δx 的極限。 因此導數又稱為“微商”。
】
瞧,微積分在生活中也可以有應用,這也是微積分的實用之處。數學是有趣而美妙的。你是否這樣覺得呢?(:……這篇文章我是希望盡量寫的通俗易懂,但由于本人水平十分有限,不免有許多錯誤及不足之處,或者你仍然看不懂這篇文章,還請各位見諒。。)
電子版: |
-

-
微積分入門之斜率與導數.pdf
2016-6-20 22:26 上傳
點擊文件名下載附件
下載積分: 黑幣 -5
364.36 KB, 下載次數: 14, 下載積分: 黑幣 -5
|