提高初學者PID原文地址:
http://brettbeauregard.com/blog/ ... s-pid-introduction/
提高初學者的PID:
這里是第一次接觸PID需要學習的公式:
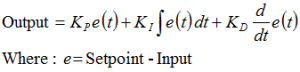
它能引導大多數人寫出如下的PID控制器代碼:
- /*working variables*/
- unsigned long lastTime;
- double Input, Output, Setpoint;
- double errSum, lastErr;
- double kp, ki, kd;
- void Compute()
- {
- /*How long since we last calculated*/
- unsigned long now = millis();
- double timeChange = (double)(now - lastTime);
- /*Compute all the working error variables*/
- double error = Setpoint - Input;
- errSum += (error * timeChange);
- double dErr = (error - lastErr) / timeChange;
- /*Compute PID Output*/
- Output = kp * error + ki * errSum + kd * dErr;
- /*Remember some variables for next time*/
- lastErr = error;
- lastTime = now;
- }
- void SetTunings(double Kp, double Ki, double Kd)
- {
- kp = Kp;
- ki = Ki;
- kd = Kd;
- }
Compute()被稱作定期或不定期的,它工作非常正常。雖然這個系列不是“工作的最好的”。如果我們想做出和工業PID控制器相近的驅動器,我們需要解決幾個問題:
Sample Time(采樣時間)——如果這是一個固定的時間間隔,PID算法的功能實現將是非常好的。如果已知了這個間隔時間,代碼中也可以簡化一些內部的數學運算。
Derivative Kick(微分的過沖)——不是最大的問題,但是很容易解決,所以我們也將處理這個問題。
On-The-Fly Tuning Changes——好的PID函數是當調整參數的時候不會干擾內部運算的。
Reset Windup Mitigation(緩解積分飽和)——我們將會了解什么是積分飽和,并且在有利的方向上進行解決方案的實施。
On/Off (Auto/Manual)(開關-自動或手動)——在大多數應用中,有時候我們希望關閉PID控制器手動調節輸出而不受控制器的干涉。
Initialization(初始化)——當控制器打開的時候我們希望是“無擾切換”,即我們不希望輸出值忽然變成一個新的值。
Controller Direction(控制器的方向)——這是最后一個不是在魯棒本身名稱下的變化。它是為了確保用戶能輸入正確的調優參數而設計的。
一旦我們解決了這些問題,我們將有一個對PID算法深刻的了解。我們還會擁有最新的Arduino PID控制庫。所以不管你是想自己寫出自己的PID算法還是想去了解PID算法里到底發生了什么,我希望這些都能幫上你。現在我們開始旅程吧。
提高初學者的PID——采樣時間
初學者的PID被稱作不規則的,這就有了以下兩個問題:
》你沒有從PID中得到一致的狀態特性,因為有時它是非常快的變化,有時卻沒有。
》你需要額外的數學運算解決微分和積分,它們都同時依賴于時間的變化。
解決方法:
確保PID定義在一個固定的時間間隔里。我這樣做的原因是讓compute指令每個周期都被調用一次。根據之前設定好的采樣周期,PID決定是該計算還是立刻返回值。
一旦我們知道了PID是在一個恒定的時間內運算,微分和積分也就變得簡單了。
代碼:
- /*working variables*/
- unsigned long lastTime;
- double Input, Output, Setpoint;
- double errSum, lastErr;
- double kp, ki, kd;
- int SampleTime = 1000; //1 sec
- void Compute()
- {
- unsigned long now = millis();
- int timeChange = (now - lastTime);
- if(timeChange>=SampleTime)
- {
- /*Compute all the working error variables*/
- double error = Setpoint - Input;
- errSum += error;
- double dErr = (error - lastErr);
- /*Compute PID Output*/
- Output = kp * error + ki * errSum + kd * dErr;
- /*Remember some variables for next time*/
- lastErr = error;
- lastTime = now;
- }
- }
- void SetTunings(double Kp, double Ki, double Kd)
- {
- double SampleTimeInSec = ((double)SampleTime)/1000;
- kp = Kp;
- ki = Ki * SampleTimeInSec;
- kd = Kd / SampleTimeInSec;
- }
- void SetSampleTime(int NewSampleTime)
- {
- if (NewSampleTime > 0)
- {
- double ratio = (double)NewSampleTime
- / (double)SampleTime;
- ki *= ratio;
- kd /= ratio;
- SampleTime = (unsigned long)NewSampleTime;
- }
- }
在第10和第11行,如果它的時間可以計算出來,那就將由算法本身決定。因為我們現在知道樣本之間的時間是相同的,我們并不需要不斷乘以時間的變化。我們只需要適當調整Ki和Kd(30和31行),雖然在數學上的結果是等價的,但更有效。
雖然這樣做又一個小小的波動。如果用戶在操作過程中決定改變采樣時間,Ki和Kd將需要重新調整來以對這一新的變化做出反應。這就第39-42行代碼所處理的問題。
另外請注意我在第29行將采樣時間轉換成秒s了。嚴格的的說這是沒有必要的,只是允許用戶輸入的Ki和Kd是uint型的s而不是ms。
|