一實驗要求:學習PID控制器的基本原理,掌握PID參數的物理調節規律,通過仿真驗證PID調節過程。選擇例題中的任意兩個實驗進行仿真研究,改變參數后觀察系統的動態性能和穩態性能的變化,確認是否和理論分析一致。 二實驗內容實驗一:選擇chap-9.m作為pid調節。 1代碼: %PID Controller with changing integration rate
clear all;
close all;
%Big time delay Plant
ts=20;
sys=tf([1],[60,1],'inputdelay',80);
dsys=c2d(sys,ts,'zoh');
[num,den]=tfdata(dsys,'v');
u_1=0;u_2=0;u_3=0;u_4=0;u_5=0;
y_1=0;y_2=0;y_3=0;
error_1=0;error_2=0;
ei=0;
for k=1:1:200
time(k)=k*ts;
rin(k)=1.0; %Step Signal
%Linear model
yout(k)=-den(2)*y_1+num(2)*u_5;
error(k)=rin(k)-yout(k);
kp=0.45;kd=12;ki=0.0048;
A=0.4;B=0.6;
%T type integration
ei=ei+(error(k)+error_1)/2*ts;
M=1;
if M==1 %Changing integration rate
if abs(error(k))<=B
f(k)=1;
elseif abs(error(k))>B&abs(error(k))<=A+B
f(k)=(A-abs(error(k))+B)/A;
else
f(k)=0;
end
elseif M==2 %Not changing integration rate
f(k)=1;
end
u(k)=kp*error(k)+kd*(error(k)-error_1)/ts+ki*f(k)*ei;
if u(k)>=10
u(k)=10;
end
if u(k)<=-10
u(k)=-10;
end
%Return of PID parameters
u_5=u_4;u_4=u_3;u_3=u_2;u_2=u_1;u_1=u(k);
y_3=y_2;y_2=y_1;y_1=yout(k);
error_2=error_1;
error_1=error(k);
end
figure(1);
plot(time,rin,'b',time,yout,'r');
xlabel('time(s)');ylabel('rin,yout');
figure(2);
plot(time,f,'r');
xlabel('time(s)');ylabel('Integration rate f');
2實驗結果 在沒有更改代碼的情況下,實驗的效果如圖一所示。
 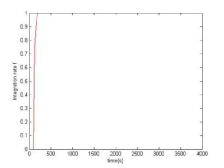 圖一 圖一
改變kp(1)增大kp,理論上可以看到pid調節的更快更陡。實際效果如圖2。Kp=3. 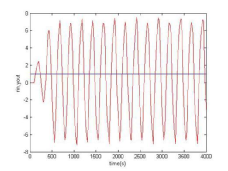 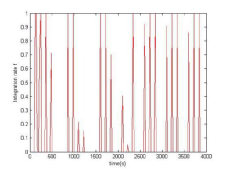 圖2 實際上產生了自激震蕩,說明kp不能調的過大,否則系統會不穩定。 (2)減小kp,理論上系統調節緩慢,會產生超調量,調節曲線不平滑,有毛刺。Kp=0.1 圖3 實際上也證明比例系數太小,系統變化時調節相對緩慢。 改變kd(1)增大kd,理論上系統穩定時波動很大,精度不高,且有很多毛刺與抖動。Kd=30. 圖4 實際上系統開始調節時會有些尖峰,調節曲線不平滑。 (2)減小kd,理論上系統調節穩定時變化緩慢,會有些超調量。Kd=3. 圖5 實際上也可以看出減小kd對系統影響不大,只是在系統剛進入穩定狀態時有一個小小的超調量。 改變ki(1)增大ki,積分變大,系統系統變得不穩定,抖動波動很厲害。 圖6 實際上可以其變化幅度大,超調量很高,系統很不穩定。 (2)減小ki,系統調節變慢,系統可能無法調節。 圖7 系統無法達到設定的穩態值,無法調節。 實驗二:選擇char2_1.m作為實驗 1代碼: %Series System Control
clear all;
close all;
ts=2;
sys1=tf(1,[10,1]);
dsys1=c2d(sys1,ts,'z');
[num1,den1]=tfdata(dsys1,'v');
sys2=tf(1,[10,1]);
dsys2=c2d(sys2,ts,'z');
[num2,den2]=tfdata(dsys2,'v');
dph=1/zpk('z',ts);
Gc2=dph/(dsys2*(1-dph));
[nump,denp]=tfdata(Gc2,'v');
u1_1=0.0;u2_1=0.0;
y1_1=0;y2_1=0;
e2_1=0;ei=0;
for k=1:1:2000
time(k)=k*ts;
r1(k)=1;
%Linear model
y1(k)=-den1(2)*y1_1+num1(2)*y2_1; %Main plant
y2(k)=-den2(2)*y2_1+num2(2)*u2_1; %Assistant plant
error(k)=r1(k)-y1(k);
ei=ei+error(k);
u1(k)=1.2*error(k)+0.02*ei; %Main Controller
e2(k)=u1(k)-y2(k); %Assistant Controller
u2(k)=-denp(2)*u2_1+nump(1)*e2(k)+nump(2)*e2_1;
d2(k)=0.01*rands(1);
u2(k)=u2(k)+d2(k);
%----------Return of PID parameters------------
u1_1=u1(k);
u2_1=u2(k);
e2_1=e2(k);
y1_1=y1(k);
y2_1=y2(k);
end
figure(1); %Assistant Control
plot(time,u1,'b',time,y2,'r');
xlabel('time(s)');ylabel('u1,y2');
figure(2); %Main Control
plot(time,r1,'b',time,y1,'r');
xlabel('time(s)');ylabel('r1,y1');
figure(3);
plot(time,d2,'r');
xlabel('time(s)');ylabel('disturbance');
2實驗效果 在沒有更改遠代碼的情況下,實驗的結果如下所示 圖8 第3個圖是隨機數的隨時間的分布。 同理,改變kp,ki的值,系統會發生改變。 改變kp (1)增大kp,系統變化會更快,會有超調量。Kp=3. 圖9 實際沒有發現系統有超調量,但在系統開始調節得時候會會產生尖峰脈沖,系統調節很快。 (2)減小kp,系統調節緩慢,但系統穩定。 圖10 結果可以看出系統調節很穩定,但調節時間有點長。 該變kd (1)增大ki,系統很快達到穩定,調節速度快.ki=0.2 圖11 結果顯示系統在轉換開始時系統產生了尖峰脈沖,然后很快地達到穩定。 (2)減小ki,系統會很慢的達到穩定.ki=0.005。 如圖12 結果顯示系統經過相當漫長的時間達到了穩定狀態。 三實驗感想通過此在MATLAB上運用pid,對pidd的實際作用有了基本了解。對于kp,要選取的合適,不能過大,否則會產生震蕩,過小可能會產生超常量,調節緩慢。對于kd,太大了產生毛刺抖動,太小了會有些超常量。對于ki,太大了調節很快,但會產生過沖,尖峰脈沖,太小了調節很慢,可能無法調試達到穩定狀態。 總結這三點,在調試pid時,kp應從小到大調試,kd從小到大調試,ki從小到大調試。每次只調一個參數,直到最滿意的時候,再調下個參數。
|