1. 電力工程，發電輸電用電，正弦量使設備簡單，效率高，經濟

2. 實驗室易于產生標準的正弦量

3. 有一套成熟的正弦電路的算法

4. 正弦量可以利用傅里葉級數分解為不同頻率的正弦量

對于正弦的使用以及電路分析有這樣的解釋：

對電路的分析其實就是對電路的建模，包括對每個元器件的建模。純阻性元件的數學模型很簡單，只有一個方程。而理想電感的方程會復雜一點，電壓電流滿足一個微分方程，而且還有關于磁鏈的方程。對于非線性的二極管等等，就有更復雜的數學模型。
數學模型建立起來之后就要求解。在求解過程中，人們發現，只有e^x和正弦函數具有一個特殊的性質，那就是不管求導多少次，都滿足函數的相似性。人們就開始研究，能否把輸入都用正弦信號或者指數信號的疊加代替，帶入電路的數學模型之后，計算非常簡便，得到輸出之后，再把輸出恢復成實際的信號。這就是傅立葉和拉普拉斯解法。
在用正弦信號求解的時候，指數函數和正弦函數又有一個牛逼的公式將兩者聯系起來，這就是歐拉公式，這樣正弦函數的相位信息就可以放到指數函數中去。

所以與其相關的算法如期而至

首先，時域算法，最容易理解，首先描述正弦量的是時域的算法（其定義的時候就是用的時間，隨時間按正弦規律變化的電壓和電流就是正弦量）  基本的單位有：

     頻率，周期，角頻率，瞬時值，最大值，有效值

     相位（瞬時值變化進程）

     初相位

     相位差（前提，頻率相同，反映了兩個正弦量變化進程差異，而非產生波形先后，超前  滯后   同相  反相正交）

  ①時域——相量   （將時域分析 換為  頻域分析）

     細節一點，在時域的正弦表示中，根據歐拉公式，轉化為了相量的形式，這其中，相量形式保持了原來正弦量的 幅值、初相位信息，即

     兩者聯系為      通過歐拉公式  實數范圍的正弦時間函數和復數范圍的復指數常數一一對應

                             但是需要注意的是，此時，我們取到的僅僅是復指數的實數部分，而且不研究旋轉因子e^jwt ,原因是，在線性的電路中，全部的穩態響應也是同頻率的正弦函數，沒有新的頻率，w顯然不是研究問題的中心，也就在相量分析中放在了一邊。

       兩者的區別為   相量！=正弦量，只能表示兩個要素（幅值與初相位），沒有ω

       學習了相量分析中的疊加原理和微分原理，值得注意的是，正弦量的微分為同頻正弦量，對應的相量為原相量乘以 jω，但不能說，相量的導數是相量乘以jω，因為，這是對于正弦量的求導，相量不是t的函數。可以感性的了解到，對于原來正弦量的t的求導，表現在相量上出來一個與時間有關的jω也是情理之中。

       使用條件    相量法只適用于激勵為同頻正弦量的非時變線性電路

       但是為啥這叫頻域分析呢？
        不是已經把w給忽略了么？  可以這樣理解，之所以略去，就是因為相當于強調了，我分析就是在頻率不變的情況下分析的！這是一個前提！

       好吧，還是知乎http://zhuanlan.zhihu.com/#/wille/19763358（00）大神膜拜

      但是，前面所說的全都是一個頻率，可以看做，對應頻域就是一個w的正弦。

      相量法之所以分離出來，在一定程度是為了區別復頻域，要知道復頻域里面是有s的，其中有頻率的量綱，頻域是以頻率為變量的，而相量法是頻域特殊的一種，即w直接不變了，直接叫相量法肯定更有代表性。

      這應該夠清楚的了

 ② 時域——復頻域 （買噶的）

      這玩意兒糾結我很久了，是該給他算賬的時候了。

      時域線性常微分方程經過拉氏變換到拉氏，度娘如是說。

      拉式變換？啊，我的積分變換，咋么不好好學 ，坑爹的學校還不讓學信號與系統。。。好吧，把人家的課程知識偷過來看看

      頓時感覺是不是瞬間腦補了一下?

      如果沒有，解釋一下：

      簡要的說一下啥是傅里葉和拉普拉斯，

                   傅里葉，一個時域的函數，通過乘上一個e^jwt ,為啥憑空乘個這東西呢？看人家后面怎么做：

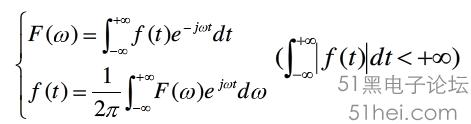
                     簡直機智！把原來的函數在原來的t的時域上面進行積分，獲得了關于w的函數，也就是頻域上面的函數（請原諒我的遲到的理解，，，本應該在積分變換就應該理解的東西。。。），這樣，這樣就實現了對于時域與頻域的變換。

                   而拉普拉斯，則是對于傅里葉函數成立條件太苛刻而進行的拓展，在乘以e^jwt 的基礎上，直接乘以e^σ，保證原來的函數是在t的時域上面是收斂的，也就是通過積分可以獲得一個不是無窮大的函數，而這個函數的變量，從原來的w，即頻域，拓展到了復頻域s上面，這個s不僅僅可以描述傅里葉的頻率，更可以可以信號的衰減震蕩穩定等關系（自控系統的穩定性分析）

        兩者講完了，但是在電路分析中對應有什么呢？自控系統為毛也有這東西呢？

        網上這解釋比較直觀：

               拉普拉斯為什么可以求解微分方程？

               拉普拉斯變換提供了一種變換定義域的方法,把定義在時域上的信號（函數）映射到復頻域上（要理解這句話,需要了解一下函數空間的概念--我們知道,函數定義了一種“從一個集合的元素到另一個集合的元素”的關系,而兩個或以上的函數組合成的集合,就是函數空間,即函數空間也是一個集合；拉普拉斯變換的“定義域”,就是函數空間,可以說,拉普拉斯變換就是一種處理函數的函數.由于拉普拉斯變換定義得相當巧妙,所以它就具有一些奇特的特質）,而且,這是一種一一對應的關系（只要給定復頻域的收斂域）,故只要給定一個時域函數（信號）,它就能通過拉普拉斯變換變換到一個復頻域信號（不管這個信號是實信號還是復信號）,因而,只要我們對這個復頻域信號進行處理,也就相當于對時域信號進行處理（例如設f(t)←→F(s),Re>a,則若我們對F(s)進行時延處理,得到信號F(s-z),Re>a+Re[ z],那么就相當于我們給時域函數乘以一個旋轉因子e^zt,即f(t)e^zt←→F(s-z),Re>a+Re[ z]；只要對F(s-z)進行