若當前時刻為12點整，則時針和分針均指向刻度12。隨后，因為兩者的角速度不同，因此逐漸分開，但經過1小時后，分針轉過一周，有趕上時針的趨勢，因此兩者漸漸重合。1點整時，分針指向刻度12，時針指向刻度1；1點5分時，分針恰指向刻度1，時針則超過刻度1。由于表盤上共有12大格（介于刻度1，2，3…，12之間），每個大格又被分為5小格，則時針前進1大格為1小時，前進1小格為12分鐘。由此可以看出，1點5分時，時針位于刻度1后第1小格的5/12處；而在1點零6分時，分針恰指向刻度1后第1小格處，時針介于第1小格的6/12=1/2處。因此，1點零5分時，時針在分鐘之前；1點零6分時，分針已超過時針。兩者重合發生在這兩個時刻之間。

算術求解：其實該鐘表問題類似于算術中的“追擊”問題。只要選擇好運動的起點，便可以套用公式：追擊時間=路程/速度差求解。分針的角速度為1（小格/分鐘），時針的角速度為其1/12（小格/分鐘）。兩者速度差為11/12（小格/分鐘）。我們選擇運動起點為1點整，此時分針落后時針5小格，因此：

即兩者重合時間為1點5分27.3秒。

       代數求解：分針角速度為時針角速度的12倍，因此若設時針從1點整起到兩針重合時走過的角度為x（單位：小格），則分針走過的距離為12x；另外，注意到1點整時，分針指向刻度12，時針指向刻度1，兩者相差5小格。建立方程如下：

則

分針走過了5.45小格，結果同算術求解。

       等比數列公式求解：高等數學求解的思考過程是在初始條件下，考慮分針追擊時針的過程。1點整時，時針（處于刻度1處）超前分針（處于刻度12處）5小格；則5分鐘后分針到達刻度1，時針前進了5/12小格；下一次追擊，分針前進5/12小格，時針前進（5/12）/12小格；如此下去，則兩者最終相差為無窮小量，即分針追上時針。在此過程中，分針走過距離為：

答案同算術、代數解法。

分析求解：最開始我們已分析出12點整后，分針、時針將于1點5分后1點6分之間相遇，但我們尚不知準確的時刻。繼續按照這個思路分析，則在2點整后，兩者相遇發生2點10分之后；3點整后，兩者相遇發生3點15分之后；4點整后，兩者相遇發生4點20分之后……兩者12小時內最后一次重合發生在下一個12點整，其間共發生12次重合。又因為時針、分針都是勻速轉動，因此每次重合間時間段相等。這也就是說，每次間隔為12/11大格（代表小時），或者60/11小格(代表分鐘)。依次重合的時間為：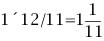

小時，而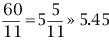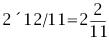

小時，而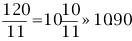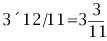

小時，而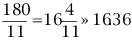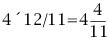

小時，而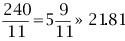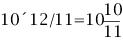

………

小時，而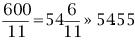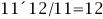

小時。

由此我們得到了12小時內每次時針、分針重合的時刻。

       由上面四種可以看出不同解法的思維特點。對問題進行正確的分析時各種解法的基礎，但是算術解法和代數解法側重點在于確立一個初始狀態和終了狀態，并通過兩者的等值關系求解。而高等數學方法則是將上述追擊過程直接通過一個無窮級數計算，并根據級數的收斂性得出結果。因此，雖然計算過程看似復雜，然而思考的過程確簡單明了。分析求解方法則是分析了時針、分針重合的特點，通盤考慮求解，也具有鮮明的特點。