在日常生活中,我們一直在做著“模式識別”。例如,迎面走來一個人,我們可以很快的判斷出,這是“女”的或者是“男”的。這通常是通過人類的性別特征((De)Merkmal,(Eng)feature)做出這樣判斷的。例如是否有喉結和胡須,胸部是否突出等。
對于人類來說,這樣的“模式識別”(分類判斷)再簡單不過了,可是這卻是大腦高級功能的具體體現。要讓計算機也能做到這一點,就非常不容易了。
而模式識別這門學科就是研究如何讓計算機自動根據從環境中所檢測到的信號對客體做出某種判斷。(注:客體,為被進行分類的物體。)“基于統計”的意思是,進行判斷的原理是基于概率統計學的。例如,當迎面走過來的人,既有胡須,胸部又突出時,按照模型判斷其是女人的概率為0.75,是男人的概率為0.25,則判斷結果了,此人是“女”的。
現在按照學習的講義,一章章的進行復習,并整理其重點。Inhalt (課程內容)
?? Einführung (導論)
?? Elemente der Wahrscheinlichkeitsrechnung (概率原理)
?? Bayes’sche Entscheidungstheorie (貝葉斯判定理論)
?? Parametersch??tzung (參數估計)
?? Nichtparametrische Dichtesch??tzung und Klassifikation (非參數的密度估計和分類)
?? Lineare Methoden der Merkmalsreduktion (削減特征的線性方法)
?? Lineare Klassifikatoren (線性分類)
?? Expectation Maximization und das Lernen von Mischverteilungen (期望最大化和混合分布的學習)
?? Support Vector Machines (支持向量機)
?? Modell-Auswahl und Bewertung (模型的選擇和評估)
第一章,導論。最典型的模式識別是如何進行的呢?
以如何判斷男女的為例說明,
1,設置攝像頭,拍攝照片
2,照片的前期處理,例如去除背景噪音,將照片中的人相部分切割出來等。
3,提取出特征:1)高度 2)亮度 等
4,根據所提取出的特征值,使用分類器進行分類。
(注,為什么在這里不用之前提到的喉結等特征呢? 這是因為喉結本身即是一個很高級的概念了。一張黑白照片可以理解為一個矩陣。每個像素的灰度值即為矩陣的各個值。所以最基本的特征值為,像素的灰度值。所有的信息都是從這個矩陣中提取出來的。例如高度可以定義為被占用的像素在縱向方向上的最大距離差。)
下面一個實際的例子進一步說明。
如圖1所示,為大馬哈魚和鱸魚的特征值比較(在此例中特征值為同一照明環境中的光亮程度)
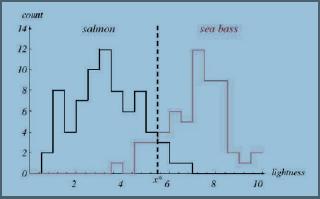
圖1
圖1說明:橫軸為魚的亮度,縱軸為魚的數量。黑色和紅色的直方圖為根據實驗得到的關于亮度的分布直方圖。黑色的為大馬哈魚的,紅色的為鱸魚的。可以看出,總體上來說,鱸魚的亮度要比大馬哈魚的要高。
從圖中很明顯的可以看出,在圖中虛線的左邊部分,大馬哈魚的概率要高于鱸魚(黑色曲線在紅色曲線上方),而到了虛線右邊則鱸魚的概率要高于大馬哈魚。
我們取圖中虛線為亮度的閥值作為判定標準。(即,大于該閥值的判定為鱸魚,否則為大馬哈魚。)
這個例子說明了如何進行的最基本的理念,即,概率大者勝。而整個模式識別就是研究如何建立一個高效的,錯誤少的判定模型。這將在之后的幾章逐步介紹。
第二章,概率原理
前面說了,模式識別的基本理念是“概率大者勝”,那么在開始之前,進行一些概率原理的介紹是必要的。有興趣的可以簡單看一下。
2.1最重要的一些概念,包括:
1,條件概率(Bedingte Wahrscheinlichkeiten)
P(B|A),即當A發生時,B發生的概率。
2,聯合概率(Verbundwahrscheinlichkeiten)
P(A,B),即A和B同時發生時的概率。
P(A,B) = P(B|A)P(A) = P(A|B)P(B)
當A和B統計無關時P(A,B) = P(A)P(B)
3,貝葉斯定理(Das Bayes-Theorem)
P(B|A) = P(A|B)P(B)/P(A)
2.2 離散隨機變量
概率函數(Die Wahrscheinlichkeitsfunktion)
期望 μ或E[x](Erwartungswerte)
方差 σ^2或Var[x](die Varianz)Var[x] = σ^2 = E[(x ?? μ)^2]
成對的離散隨機變量(Paare diskreter Zufallsvariablen)pij = Pr(x = vi, y = wj) ,用于有多個特征時。
協方差(Die Kovarianz)σxy = E[(x ?? μx)(y ?? μy)],用于描述變量x和y的概率相關性。當它們無關時等于0.
隨機向量(Zufallsvektoren)x = [x1, x2, . . . , xd]T 注:T表示轉置矩陣
P(x1, x2, x3, x4, x5) = P(x1, x2, x3, x4|x5)P(x5)
= P(x1, x2, x3|x4, x5)P(x4|x5)P(x5)
= ...
2.3連續隨機變量
分布密度(Die Verteilungsdichte),對連續的隨機變量來說,其概率大小已經沒有意義了。因為其總是無限趨近于0。所以我們使用分布密度來表示概率大小。密度越大,概率越大,在某個區間內的概率為分布密度在該區間內的積分(當取值為從負無窮大到α時,即為分布函數(Die Verteilungsfunktion)F(α))。
2.4正態分布(Normalverteilung)
有興趣的就看百度里的解釋吧。(其實更喜歡wiki,不過好像國內有的時候打不開)
2.5馬氏距離(Mahalanobis-Abstand)
歐氏距離和馬氏距離
2.6 相關聯隨機變量的多變量正態分布
還有很多進一步的說明和概念,因本文主要是為了自己復習整理重點,所以在此就不一一細說了。
*第三章:Bayes’sche Entscheidungstheorie (貝葉斯判定理論)
回顧之前的將魚進行分類的例子。我們可以用一種最直接的判斷方法,即,此次捕撈中,哪種魚的概率大就判斷所有的魚為該種魚。很明顯這樣的判斷方法太過于簡單。因為被捕撈的概率和魚本身沒有很直接的關聯。更好的方法就是,選取和魚的種類直接相關的物理特征值,例如長度,重量,亮度等等,作為判定的依據。
以亮度為例:
如果 P(ω1|x) > P(ω2|x) → 判定為ω1
如果 P(ω1|x) < P(ω2|x) → 判定為ω2
其中,ω1,ω2為種類,P(ω1|x)為亮度為x時,ω1的分布密度。
這樣的分類稱為最大后驗概率規則(Maximum-a-posteriori-Regel(MAP))。
由貝葉斯定理我們知道
P(ωj|x) = p(x|ωj) · P(ωj)/p(x)
其中,P(ωj|x)為后驗概率,即;p(x|ωj) 為似然(即,可能性);P(ωj)為先驗概率;而p(x)與模式識別沒有什么關系。
上述概念在百度百科中的注解為:
1,先驗概率是指根據以往經驗和分析得到的概率,如全概率公式,它往往作為"由因求果"問題中的"因"出現。在這里是此次捕撈中,兩種魚所占的比例。先驗概率通常是根據歷史資料進行的猜測。
"的信息后洲正的概率,如貝葉私中的,是"執果尋因"問題中的"因"。因為,是根據先驗概率求出來的,所以稱為后驗概率。
當無法猜測出各種魚的比例時,則可以采用最大似然判定規則(Maximum-Likelihood-Regel(ML))
如果p(x|ω1) > p(x|ω2) → 判定為ω1
如果p(x|ω2) > p(x|ω1) → 判定為ω2
錯誤概率的計算(Berechnung der Fehlerwahrscheinlichkeit)
很顯然上面的判定規則都有誤判的情況出現,那么錯誤的概率又是多大呢?我們如何才能降低出錯的概率呢?
以只有兩個種類的分類問題為例子說明。
對于只有兩類的分類問題來說,誤判指的是以下2種情況:
1,α2|ω1; 即 x ∈ R2|ω1,也就是說,本來是ω1,但是判定為ω2;
2,α1|ω2; 即 x ∈ R1|ω2,也就是說,本來是ω2,但是判定為ω1。
而總的誤判概率則為:
P(error) = P(x ∈ R2, ω1) + P(x ∈ R1, ω2)
用圖可以很直觀的理解上面的概念。
如圖2所示,為根據MAP規則進行分類的圖。
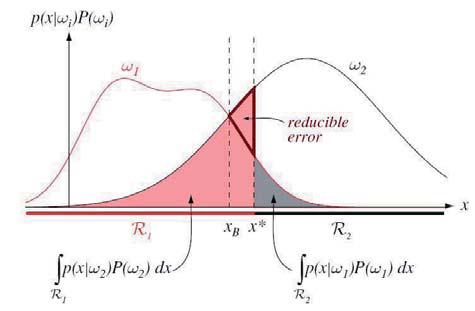
圖2說明,橫軸為特征值x,縱軸為后驗概率。紅色曲線為ω1的分布密度函數,黑色曲線為ω2的分布密度函數。紅色和灰色區域為誤判的情況,其面積為誤判概率。
隨著虛線(判定閥值)從右向左移動,錯判的概率在減小(紅色的粗框三角形區域為減少的部分)。
至此,貝葉斯判定理論算是基本介紹完了。當然,這只是最簡單的例子,在實際應用中會比這個復雜的多。
第三章中進一步重要的內容還有:
Diskriminanzfunktionen (第四次習題內容)
Klassifikation auf der Basis von Gruppen benachbarter Pixel (第五次習題內容)
Neyman-Pearson-Test (第四次習題內容)
第四章,參數估計(待續)
第五章,期望最大化和混合分布的學習(待續)
第六章,非參數的密度估計和分類(待續)
第七章,線性分類(待續)
第八章,支持向量機(待續)
第九章,削減特征的線性方法(待續)
注:本文的德語講義部分均摘自呂貝克大學ISIP學院A. Mertins教授的Stat. Mustererkennung的講義中。如有轉載,請注明來源。
|