實驗項目總共十二個,包括:
系統建模和穩定性分析
頻域法復合校正
根軌跡校正
復合校正的分析及改進
PID 法校正
狀態反饋控制
頻域法校正
不同狀態下狀態反饋控制效果比較
根軌跡法復合校正
LQR 控制
PID 法復合校正
開環頻率特性測試
倒立擺的控制算法多種多樣,各種方法都有其各自的領域及重點,通過算法的比較,可以看出它們彼此之間的一些優缺點
倒立擺實驗內容基本原則:應能滿足任務書所選控制對象的技術性能指標要求;本設計以單片機、DSP以及計算機為控制器;要求獨立完成所選課題的控制系統方案設計、硬件電路設計、控制軟件設計、系統建模、數值仿真或實驗驗證分析;獨立完成設計文檔。 基本步驟:系統調研分析;對控制系統進行設計之前,首先要查閱一定量的文獻資料,明確設計任務要求,控制對象的特點與控制工藝要求等。微處理器選擇; 本設計提供兩種微處理器供選擇:單片機和DSP。 硬件電路設計:根據控制對象特點和設計要求,獨立完成系統硬件線路原理圖設計和PCB版圖設計。硬件電路設計包括:單片機或DSP基本系統設計、輸入\輸出電路設計、人機接口電路設計等。 系統程序設計首先根據控制對象控制工藝要求,畫出系統控制軟件程序流程圖,在此基礎上完成系統全部程序設計工作。包括:人機界面程序和實時控制程序。 系統建模與仿真:根據所選的控制對象,建立控制對象模型,應用Matlab仿真軟件進行數值仿真,觀測分析PID控制參數(比例系數、積分系數和微分系數)對控制性能的影響,記錄仿真結果。 實驗驗證:部分控制對象可以在計算機控制技術實驗室的實驗平臺是進行實物實驗驗證。獨立完成系統搭建工作,調整PID控制參數(比例系數、積分系數和微分系數),記錄實驗結果,觀測分析PID控制參數對控制性能的影響。
第3章 倒立擺系統建模
3.1倒立擺系統建模概論倒立擺系統其本身是自不穩定系統,實驗建模存在一些問題和困難,在忽略掉一些次要的因素后,倒立擺系統是一個典型的運動的剛體系統,可以再慣性坐標系中運用經典力學對它進行分析,來建立系統動力學方程。在忽略掉了空氣阻力和各種摩擦力之后,可以講一階倒立擺系統抽象成小車和均勻桿組成的系統,一階倒立擺系統的結構示意圖如下: 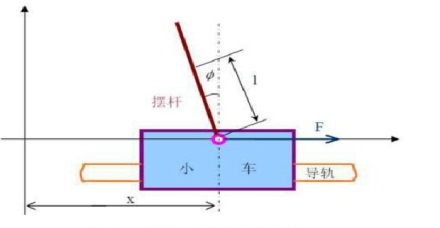
圖2 一階倒立擺系統的結構示意圖 定義的參數為: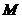 小車質量 小車質量 - 擺桿質量
-
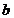 小車摩擦系數 小車摩擦系數
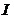 擺桿慣量 擺桿慣量
 加在小車上的力 加在小車上的力
 小車位置 小車位置
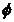 擺桿與垂直向上方向的夾角 擺桿與垂直向上方向的夾角
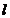 擺桿轉動軸心到桿質心的長度 擺桿轉動軸心到桿質心的長度
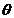 擺桿與垂直向下方向的夾角(擺桿初始位置為豎直向下) 擺桿與垂直向下方向的夾角(擺桿初始位置為豎直向下)
得到小車和擺桿的受力圖: 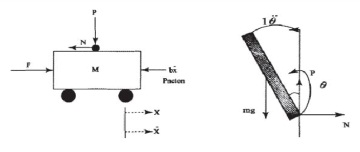
圖3 小車和擺桿的受力圖 系統建模可以分為兩種:機理建模和實驗建模。機理建模是在了解研究對象的運動規律基礎上,通過物理、 化學的知識和數學手段建立起系統內部的輸入—輸出狀態關系。 實驗建模是通過在研究對象上加上一系列的研究者事先確定的輸入信號,激勵研究對象并通過傳感器檢測其可觀測的輸出,應用數學手段建立起系統的輸入—輸出關系。 這里面包括輸入信號的設計選取、 輸出信號的精確檢測、 數學算法的研究等等內容。對于倒立擺系統,經過小心的假設忽略掉一些次要的因素后, 它就是一個典型的運動的剛體系統,可以在慣性坐標系內應用經典力學理論建立系統的動力學方程。 下面采用其中的牛頓—歐拉方法建立直線一級倒立擺系統的數學模型。 3.2倒立擺數學模型的建立分析小車水平方向所受的合力,可以得到以下方程: 設擺桿受到與垂直方向夾角? 為的干擾力Fg ,可分解為水平方向、垂直方向的干擾力,所產生的力矩可以等效為在擺桿頂端的水平干擾力Fs、垂直干擾力 Fh 產生的力矩。 對擺桿水平方向的分析可以得到式: 即: 對圖擺桿垂直方向上的合力進行分析,可得式: 即: 力矩平衡方程如下: 帶入 P 和 N,得到方程: 設?=?+?(?是擺桿與垂直向上方向之間的夾角,單位是弧度)。設? ?? 1,則可以進行近似處理: 由于: 方程可化為: 令: Ff=Fg(-sin?-?cos?)則化簡為: 即是化簡后的直線一級倒立擺系統微分方程。 帶入實際數據后,微分方程如式: 當忽略系統Ff ,系統微分方程如式: 忽略干擾力后,直線一級倒立擺系統是單輸入二輸出的四階系統,考慮干擾力后,直線一級倒立擺系統是二輸入二輸出的四階系統。其內部的 4 個狀態量分別是小車的位移 x 、小車的速度 v 、擺桿的角度? 、擺桿的角速度? 。系統輸出的觀測量為小車的位移 x 、擺桿的角度? 。其控制量為小車的加速度a ,Ff 是直線一級倒立擺運動中各種干擾因素的綜合項,可以等效為干擾力考慮。 建立系統傳遞函數 根據系統微分方程式(1-10c),轉化為關于加速度輸入量和角度輸出量的傳遞函數: 直線一級倒立擺穩定性分析 構建如圖 3.4 所示閉環系統,則系統的閉環極點為(±5.1381): 圖3-4閉環系統 由于有實部為正的極點,所以閉環系統不穩定,必須設計控制器使系統穩定。 仿真實驗 1) 在 LAB\simulink 中構建圖 3.5 所示所示系統的仿真程序 e1,默認格式 slx,加入 1m/s2的階躍信號。 圖3-5構建圖 2) 雙擊 Setup 模塊,設置 Final value 值為 1 3) 點擊“  ”,運行仿真程序 ”,運行仿真程序 4) 雙擊打開 Scope 示波器,查看仿真曲線 圖3-7仿真曲線 5) 此時系統發散,不穩定。 實驗記錄:
3.3定量、定性分析系統的性能設系統狀態空間方程為: 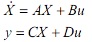
方程組對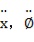 解代數方程,得到解如下: 解代數方程,得到解如下: 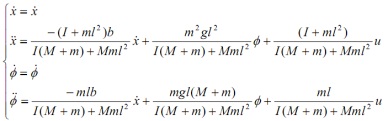
整理后得到系統狀態空間方程: 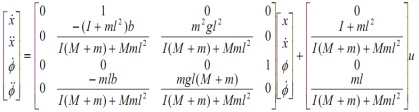
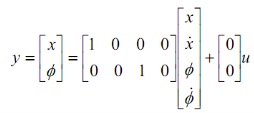
實際參數代入: 一階倒立擺系統,系統內部各相關參數為: 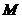 小車質量 0.5 Kg ; 小車質量 0.5 Kg ;
 擺桿質量0.2 Kg ; 擺桿質量0.2 Kg ;
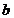 小車摩擦系數0.1 N/m/sec ; 小車摩擦系數0.1 N/m/sec ;
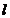 擺桿轉動軸心到桿質心的長度0.3 m ; 擺桿轉動軸心到桿質心的長度0.3 m ;
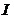 擺桿慣量0.006 kg*m*m ; 擺桿慣量0.006 kg*m*m ;
 采樣時間0.005秒。 采樣時間0.005秒。
將上述參數代入得實際模型: 擺桿角度和小車位移的傳遞函數: 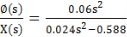
擺桿角度和小車所受外界作用力的傳遞函數: 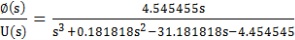
以外界作用力作為輸入的系統狀態方程: 

對系統的穩定性進行分析 在MATLAB中運行以下程序: A=[ 0 1 0 0; 0 -0.181818 2.672727 0; 0 0 0 1; 0 -0.454545 31.181818 0]; B=[ 0 1.818182 0 4.545455]'; C=[ 1 0 0 0; 0 0 1 0]; D=[ 0 0 ]'; [z,p,k]=ss2zp(A,B,C,D) z = -4.9497 0.0000 + 0.0000i 4.9497 0.0000 - 0.0000i p = 0 -5.6041 -0.1428 5.5651 k = 1.8182 4.5455 >> impulse(A,B,C,D) 系統脈沖響應 由圖可得,系統在單位脈沖的輸入作用下,小車的位移和擺桿的角度都是發散的,同時,由以上程序的零極點得極點有一個大于零,因此系統不穩定。 對系統的穩定性進行分析: A=[ 0 1 0 0; 0 -0.181818 2.672727 0; 0 0 0 1; 0 -0.454545 31.181818 0]; B=[ 0 1.818182 0 4.545455]'; C=[ 1 0 0 0; 0 0 1 0]; D=[ 0 0 ]'; >> Qc=ctrb(A,B); >> Qo=obsv(A,C); >> rank(Qc) ans = 4 >> rank(Qo) ans = 4 因此系統為完全能觀測和完全能控的。 第4章 倒立擺系統校正
4.1倒立擺系統的PID 校正 1. PID 法校正直線一級倒立擺系統 PID 的控制算法有很多,不同的算法各有其針對性。圖 5-1、圖 5-2、圖 5-3 給出了三種不同的算法。在模擬控制系統中,控制器最常用的控制規律是 PID 控制。模擬 PID 控制系統原理框圖如圖5.2 所示。系統由模擬 PID 控制器和被控對象組成。 圖 4-1 模擬 PID 控制原理圖 圖 4-2 微分先行 PID 控制原理圖 圖 4-3 偽 PID 控制原理圖 PID 控制器是一種線性控制器,它根據給定值r(t)與實際輸出值c(t)構成控制偏差e(t) 。 e(t)=r(t)-c(t) 將偏差的比例 P、積分 I 和微分 D 通過線性組合構成控制量,對被控對象進行控制,故稱為 PID控制器,其控制規律為: 寫成傳遞函數形式為: 式中: K :比例系數; TI :積分時間常數; TD :微分時間常數;控制器設計和仿真中,也將傳遞函數寫成: 式中: KP —比例系數、 KI —積分系數、 KD —微分系數。從根軌跡角度看,相當于給系統增加了一個位于原點的極點和兩個位置可變的零點。 簡單說來, PID 控制器各校正環節的作用如下: 1) 比例環節:成比例地反映控制系統的偏差信號,偏差一旦產生,控制器立即產生控制作用,以減少偏差。 2) 積分環節:主要用于消除穩態誤差,提高系統的型別。積分作用的強弱取決于積分時間常數越大,積分作用越弱,反之則越強。 3) 微分環節:反映偏差信號的變化趨勢(變化速率),并能在偏差信號值變得太大之前, 在系統中引入一個有效的早期修正信號,從而加快系統的動作速度,減小調節時間。 2. PID 參數整定方法 1) 根軌跡法 PID 的數學模型可化為: 相當于是給系統增加了一個位于原點的極點和兩個位置可變的開環零點,因此對于低階已知數學模型的系統,根據期望的性能指標可以采用根軌跡法確認 PID 參數。 2) 頻域法 對于已知頻率特性曲線的系統, PID 控制器相當于給頻率特性曲線增加了積分環節和一個二階微分環節,通過調整 PID 參數,可以改變 PID 控制器的頻率特性,進而改變閉環系統的頻率特性。 3) 湊試法 在 PID 參數進行整定時如果能夠用理論的方法確定 PID 參數當然是最理想的,但是在實際的應用中,由于各種因素影響,更多的是通過湊試法來確定 PID 的參數。 增大比例系數 P 一般將加快系統的響應,在有靜差的情況下有利于減小靜差,但是過大的比例系數會使系統有比較大的超調,并產生振蕩,使穩定性變壞。 增大積分時間 I 有利于減小超調,減小振蕩,使系統得穩定性增加,但是系統靜差消除時間變長。 增大微分時間 D 有利于加快系統的響應速度,使系統超調量減小,穩定性增加,但系統對擾動的抑制能力減弱。 在湊試時,可參考以上參數對系統控制過程的影響趨勢,對參數調整實行先比例、后積分、再微分的整定步驟。首先整定比例部分,將比例系數由小變大,并觀察相應的系統響應,直至得到反應快、超調小的響應曲線。如果系統沒有靜差或靜差已小到允許范圍內,并且對響應曲線已經滿意,則只需要比例調節器即可。如果在比例調節的基礎上系統的靜差不能滿足設計要求,則必須加入積分環節。在整定時先將積分時間設定到一個比較大的值,然后將已經調節好的比例系數略為縮小(一般縮小為原值的 0.8),然后減小積分時間,使得系統在保持良好動態性能的情況下,靜差得到消除,在此過程中,可根據系統的響應曲線的好壞反復改變比例系數和積分時間,以期得到滿意的控制過程和整定參數。如果在上述調整過程中對系統的動態過程反復調整還不能得到滿意的結果,則可以加入微分環節,首先把微分時間 D 設置為 0,在上述基礎上逐漸增加微分時間,同時相應的改變比例系數和微分時間,逐步湊試,直至得到滿意的調節結果。 3. 采用根軌跡法確定 PID 參數舉例 加 PID 控制器后角度閉環結構圖如圖所示: 圖4-4加 PID 控制器后角度閉環結構圖 角度控制系統的開環傳遞函數為: 開環極點為:±5.42, 0 開環零點為: PID 環節為系統增加了一個位于原點的極點,兩個可變的零點。系統有共有兩個零點、三個極點。三階系統可以采用根軌跡法確定 PID 參數。根據兩個零點的相對位置,可以把根軌跡分成八種,如下圖所示: 圖4-5兩個共軛零點位于右半平面 圖4-6兩個零點在實軸上,均在正極點的右側 圖4-7兩個零點在正實軸上,其中一個位于正極點右側 圖4-8一個零點在正實軸上,一個位于負實軸上 圖4-9兩個共軛零點負實部介于負極點和原點之間 圖4-10兩個負實零點介于負極點和原點之間 圖4-11兩個負實零點位于負極點左邊 圖4-12兩個共軛零點,負實部位于負極點左邊,距負極點較近 圖4-13兩個共軛零點,負實部位于負極點左邊,距負極點較遠 從上述八種圖可以看出,圖4-5、圖4-6、圖4-7、圖4-8 所示四種根軌跡,閉環系統一定有右極點,不穩定;圖4-9、圖4-10 所示,至少有兩個閉環極點位于左極點和原點之間,系統快速性不好;圖 4-11所示雖然三個閉環極點均可位于左側,但是中間一根根軌跡分支其長度有限,根軌跡增益即使發生變化很大,系統快速性也不會有很大改善;圖4-12、圖4-13可以通過調整更軌跡增益使閉環系統極點位于開懷左極點的左側,并且盡量靠近負實軸,設計出快速性、穩定性均較好的系統。 4.2 倒立擺系統的根軌跡校正 1. 根軌跡法分析直線一級倒立擺系統穩定性直線一級倒立擺單入單出系統開環傳遞函數為: 開環系統的極點為:±5.42 閉環環根軌跡如圖: 圖4-15閉環環根軌跡 由系統根軌跡圖可以看出閉環傳遞函數的一個開環極點位于右半平面,并且閉環系統的根軌跡關于虛軸對稱,這意味著無論根軌跡增益如何變化,閉環根總是位于正實軸或者虛軸上,即系統總是不穩定或臨界穩定的。 2. 零極相消法校正 對于二階系統而言,閉環極點距離虛軸越遠,系統的調節時間就越短;閉環極點距離負實軸越近,超調量就越小。不妨對系統新增加一個開環零點和一個開環極點,零點為-5.42,消去倒立擺的開環左極點,增加一個位于 40 的開環左極點。控制器為: k 為開環增益,控制系統結構圖如圖所示: 圖4-16控制系統結構圖 加控制器后系統根軌跡圖如圖所示: 圖4-17控制器后系統根軌跡圖 當k = 400,加入階躍激勵信號為 0.05m/ 時,?(s) 仿真輸出如下圖所示: 時,?(s) 仿真輸出如下圖所示: 圖4-18仿真輸出 3. 加根軌跡校正后實時控制實驗 1) 打開倒立擺系統電控箱上的電源,然后將倒立擺小車扶至導軌中間位置。 2) 在 Matlab 命令行中輸入 gtbox,打開 gtbox 工具箱中“gtbox/Inverted Pendulum/Servo MotorDriven/GLIP/GTS/One Stage/2-Root Locus”路徑下的“Root_Locus_Control_gts”程序。 圖4-19命令行圖 a) 實時控制程序程序設計簡介: 輸入目標擺桿角度, 設計閉環負反饋系統,加根軌跡校正模塊使系統,輸入目標擺桿角度信號與系統反饋角度信號比較后通過根軌跡控制器使系統滿足要求。 b) 程序模塊說明 ① 藍色模塊均為運動控制卡模塊詳見第二章 2.2 節; ② Angle Ref 模塊:目標擺桿角度; ③ Enter Ang 模塊:比較目標與實際角度差值小于 10°時該模塊連通后續模塊; ④ Slider Gain 及 Transfer Fcn1 模塊:根軌跡控制器; ⑤ Real Control 模塊:詳見第二章 2.3 節; 3) 點擊“ ”編譯程序; ”編譯程序; 4) 編譯成功后,點擊“ ”連接程序,點擊“ ”連接程序,點擊“ ”運行程序 ”運行程序 5) 程序運行后,用手扶擺桿末端扶起擺桿至豎直向上位置,此時程序進入控制,扶住擺桿末端使其維持在導軌中間位置; 6) 然后把“Step Switch”模塊打到0.05/ 時,Angle中系統輸出響應情況 時,Angle中系統輸出響應情況 圖4-20系統輸出響應圖 實驗記錄:
實驗分析及思考: 1. 系統不穩定的原因分析 直線一級倒立擺系統是小車在光滑的導軌上運動,小車上鉸鏈了一根擺桿。當擺桿被控時,小車運動的位移也受到導軌實際長度的限制。因此,輸出量除了擺桿角度外,還有一個小車運動的位移。位移與輸入量小車加速度之間的關系為: 控制系統結構如如圖所示: 圖4-21控制系統結構圖 此時位移輸出仿真圖如圖所示:橫軸單位:秒、縱軸單位:米 圖4-22位移輸出仿真圖 小車一直向一端加速,最終導致小車撞限位,擺桿不穩定。 由于倒立擺運動中,不可避免地會受到各種因素的干擾,即使在平衡狀態,角度、位移也會在一定范圍內波動。因此,可以通過在輸入端加入恒定的一個小階躍信號,補償各種干擾對倒立擺穩定造成的影響,即靜態補償的方法,使倒立擺系統靜態穩定。注意:靜態補償值的大小,與倒立擺擺桿扶起的速度、方向、導軌摩擦力等有關,需要反復湊試確定,而且每次都有所偏差。
以上圖文的Word格式文檔下載(內容和本網頁上的一模一樣,方便保存):
 倒立擺.docx
(1.13 MB, 下載次數: 13)
倒立擺.docx
(1.13 MB, 下載次數: 13)
2021-11-24 17:14 上傳
點擊文件名下載附件
下載積分: 黑幣 -5
|