上一節我們知道了什么是位式控制，這節就正式進入PID的學習。

簡單畫了一個系統的控制流程圖：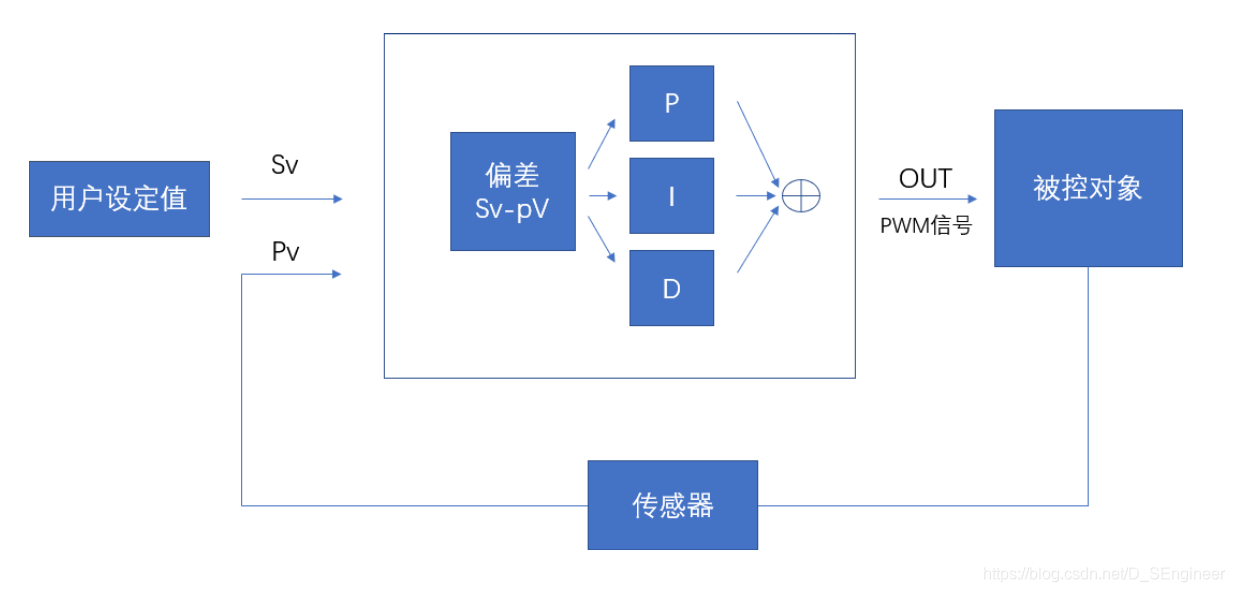

系統說明：
假設該系統是一個溫控系統，用戶可設定目標值Sv，單片機檢測了用戶輸入的值之后，通過PID算法進行計算，得出一個值去輸出PWM，PWM去控制加熱絲的電源，加熱絲就是被控對象。加熱絲旁邊有個溫度傳感器，可以實時監測加熱絲的溫度，并反饋給單片機一個當前的溫度值Pv。之后單片機將Sv和Pv進行PID運算，根據計算結果再次改變PWM的值，就這樣以此循環下去。

第一個時間點采樣值為X1，第二個時間點采樣值為X2,以此類推第k-1個采樣點采樣值為Xk-1，第k個采樣點采樣值為Xk。那么將從第一個時間點采樣的值到第k個采樣值排成一個序列如下：
X1 、 X2 、 X3 、、、 Xk-2 、 Xk-1 、Xk

P，大家都知道是比例運算。比例運算是根據當前傳感器采集的值Pv和用戶設定的目標值Sv進行比較之后，做一個比例輸出，假設當前誤差Ek = Sv - Xk，那么在單獨使用P運算時，會輸出：

這就會產生三種運算結果：
1.
當Ek > 0; => 系統沒有達到目標值 => 差值為正，當差值較大時，也就是當前測量值和目標值相差甚遠的時候，這就會使得OUTp的值變大，OUTp的值是控制PWM的占空比的。OUTp的值越大，占空比越大，平均電壓值越高，加熱絲加熱越快，使得當前值以最快的速度接近目標值，當差值較小時則相反；
2.
當Ek = 0; => 系統已經達到目標值 => 差值為0，也就是當前測量值和目標值相差為0的時候，這就會使得OUTp的值為0，OUTp的值是控制PWM的占空比的。OUTp的值為0，占空比為0，平均電壓值越也就為0，加熱絲不在進行加熱，此時加熱絲已經不受控制，不受控制就容易受外界影響而改變溫度；
3.
當Ek < 0; => 系統超過目標值 => 差值為負，也就是當前測量值已經超過目標值，PWM不可能輸出負的，因此只能不在輸出PWM，加熱絲也會處于不受控的狀態。

從運算結果可得出以下幾個結論：
1.只有當系統存在誤差了，我才控制你，如果沒有誤差我就不控制了，也就是說單獨的P運算是個一直有誤差的運算，也就是靜態誤差
2.當前值和目標值相差越大，我輸出就越大，相差越小，我輸出就小，也就是說P可以加快被控對象達到目標設定值
3.P運算只和當前值作比較，也就說P控制的是當前的狀態

以上就是P的特點。

優化：
在沒有誤差的情況下為了還能控制被控對象，往往會在后面加一個常量OUT0：

也就是說當沒有誤差時，K*Ek=0，但我最后的輸出OUTp = OUT0,還能控制被控對象，但是OUT0該設置多少就要看實際情況了，只能說有改善，但是很雞肋。如果環境變化很大，OUT0形同虛設。

將每個采樣時間點的值和目標設定值做一個差值，就能得出每次采樣的誤差值。第一個采樣時間點的差值E1 = Sv - X1，第二個時間點的差值E2 = Sv - X2，以此循環，第k-1個時間點的差值Ek-1 = Sv - Xk-1，第k個時間點的差值Ek = Sv - Xk，排成序列如下:

E1 、 E2 、 E3 、、、 Ek-2 、 Ek-1 、Ek

那么我們來看看將這些歷史誤差加到一起會有什么結論

Sk = E1 + E2 + E3 +++ Ek-2 + Ek-1 + Ek

Sk的值也會產生三種運算結果：
1.
當Sk > 0; => 所有正數的和的絕對值比所有負數的和的絕對值要大 => 從E1到Ek這么多數中，為正的個數多于為負的個數 => 也就是說在歷史采樣k次中，大多數是采樣到系統沒有達到目標值的。因為Ek >
0說明Sv > Xk ， 說明系統沒有達到目標值
2.
當Sk = 0; => 所有正數的和的絕對值等于所有負數的和的絕對值 => 從E1到Ek這么多數中，為正的個數等于為負的個數 => 也就是說在歷史采樣k次中，剛好沒有達到目標值的次數和達到目標值的次數相等
3.
當Sk < 0; => 所有正數的和的絕對值比所有負數的和的絕對值要小 => 從E1到Ek這么多數中，為正的個數少于為負的個數 => 也就是說在歷史采樣k次中，大多數是采樣到系統都達到目標值的。因為Ek <
0說明Sv < Xk ， 說明系統達到目標值

現在我們想讓這個Sk單獨加到我們的運算當中，并且做一定的放大，這里說的是放大，其實是根據系數大不大于1而定的。那么我們可以得出一個公式：

那么我們來想想，I運算會不會有不受控的時候。答案是肯定有的。當Sk等于0時，系統是不受控制的，也就說在K次的采樣結果中，達到設定目標的次數等于沒有達到目標的次數時，系統是不受控制的。

從運算結果可得出以下幾個結論：

1.只有當系統存在歷史誤差了，注意是歷史誤差，我才控制你，如果沒有歷史誤差我就不控制了，也就是說單獨的I運算也是一個有誤差的運算
2.I運算參考的是歷史數據，是對系統歷史狀態做出一個整體評估，當歷史狀態大多數都沒達到設定值時我就輸出一個大一點的信號，讓系統在之后的運行中打到目標值，當歷史狀態大多數都達到設定值的時候則相反。

以上就是I的特點，和P有點類似只不過一個是將當前值作為參考，一個是將過去值最為參考。

優化：
在沒有歷史誤差的情況下為了還能控制被控對象，往往會在后面加一個常量OUT0，雖然用處不大：

我們將積分中在k次采樣的誤差值Ek和k-1次采樣的誤差值Ek-1做差值會得到什么結論呢？

首先我們要理解Dk的含義：

Dk是這次采樣的誤差和上次采樣的誤差的差值，假如采樣時間很小，我們是不是可以把Dk看做是誤差的斜率，也就是Dk的值反映了單位時間內誤差的變化快慢。Dk越大,說明誤差變化率越大，Dk越小，則誤差的變化率越小。

再舉個例子：
S = VT （ 路程=速度*時間） 我們又知道路程的倒數是速度，導數可以理解為變化率,也就是變化的快慢。在一段時間內走了一段路，那么在任意時刻路程的導數就表示該單位時間內走過的路程,也就是速度了。

再看看上面說的Dk,假設采樣時間很短，Dk是不是就可以理解為在單位時間內誤差從Ek-1變成了Ek，相當于路程在單位時間內從S1變成了S2，那么S2-S1是單位時間內走的路程，在對單位時間求導是不是就是速度了，Ek- Ek-1是單位時間內誤差的變化值，在對單位時間求導是不是就是誤差的變化率了。

在理解了Dk的含義之后我們就可以運用I運算了，同樣的給D一個比例，放大一定倍數進行輸出：

由于OUTd和Dk只是倍數關系，因此只看Dk的變化就能知道OUTd的變化，：
1.
當Dk > 0; => 這次的誤差值比上一次的誤差值大 => 說明本次相比上次更加遠離目標值了 => 偏差越來越大
2.
當Dk = 0; => 這次的誤差值等于上一次的誤差值 => 說明本次相比上次誤差沒有變化 => 偏差不變
3.
當Dk < 0; => 這次的誤差值小于上一次的誤差值 => 說明本次相比上次更加接近目標值了 => 偏差越來越小

由于變化率本身反映的就是一種趨勢，什么是趨勢？趨勢就是根據當前的環境去預測以后會發生的事情。因此D微分運算最大的一個作用就是通過誤差的變化率去預判在下一個采樣時刻系統會有什么樣的變化，這樣就能提前做出相應的動作，而不是等待溫度達到目標值再去關閉PWM

從運算結果可得出以下幾個結論：
1.當誤差的變化率為0時，系統會不受控制
2.不能單獨存在，為什么這樣說呢。因為微分是看誤差的變化率而不是誤差本身。
舉個例子，比如下圖，目標值假設為100

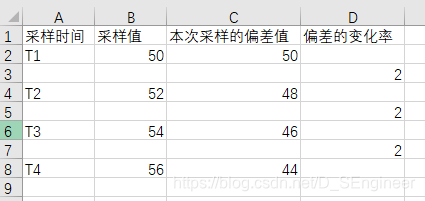
4次采樣，每次采樣的偏差值都在變化，而偏差的變化率卻一直是2，也就是說Dk=2，微分有輸出。那么假設溫度就這樣很有規律的往上加呢，那是不是當溫度到達了100度，微分還會有輸出，因為微分可不管你是多少度，只要Ek-Ek-1不等于0我就一直輸出。那如果沒有P和I的加入，只有微分是不是就會一直加熱。因此微分不能單獨存在。

3.還有一點很重要，就是微分輸出具有超前預判的功能
這一點也很好理解，剛才已經說過Dk是誤差的變化率，變化率反映的是一種趨勢，那么當Dk > 0時，Dk越大，OUTd就越大，也就是說Dk越遠離目標值，我輸出就越大，輸出越大加熱越快，加熱越快就會讓你越接近目標值，也就是說你上一次里目標越遠，我就在下一次輸出越大，讓你離目標值越近，這就是D微分運算的預判特點。

上面所講的都是在離散型的系統中才能實現的。就像我們的單片機定時采樣一樣，他不可能無時無刻的去采樣傳感器的值，只能定時去采樣，但如果這個采樣時間很短呢，是不是就可以無限接近連續型系統了。

P與當前誤差有關，當前誤差大我就輸出大，誤差小輸出小，主要是根據系統當前的狀態做出響應；I與系統的累積誤差有關，系統過去的總體表現影響現在的輸出；D與系統上一時刻的誤差變化率有關，根據上一時刻的變化率判斷系統下一個采樣時刻可能會發生的變化。

P可以提高系統響應時間，I可以消除靜態誤差，D可以預判系統的變化。