|
參數整定要求 通過整定選擇合適的參數,首先要保證系統穩定,這時最基本的要求 在熱工生產過程中,通常要求控制系統有一定穩定裕度,即要求過程有一定的衰減比,一般為4:1~10:1 在保證穩定的前提下,要求控制過程有一定的快速性和準確性.所謂快速性就是要求控制系統的動態偏差(余差)盡量的小,而快速性就是要求控制過程的時間盡可能地短. 常用整定方法 當閉環特征方程為二階時,可以通過理論計算求出各參數與衰減比的對應關系 如上圖: 被控對象的傳遞函數為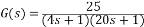 ,采用比例控制器為 ,采用比例控制器為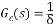 ,求解合適的比例帶δ值,使得系統衰減比為4:1; ,求解合適的比例帶δ值,使得系統衰減比為4:1; 解: 1.求得系統閉環傳遞函數為: 2. 已知衰減率φ為: 系統閉環特征方程為: 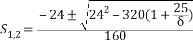 = =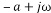 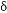 =0.665=66.5% =0.665=66.5% 工程整定方法 A 經驗法(試湊法) 試湊法的整定步驟如下所述: 1)先采用比例作用,設置積分時間T1=∞微分時間TD=0,根據經驗設置比例帶δ,將系統投入閉環運行,穩定后做階躍擾動試驗,改變比例帶δ值,使被調量的階躍響應曲線出現4:1衰減震蕩,記錄此時的比例帶δ 2)比例積分作用: 在1)的基礎上,首先將δ增大10%~20%,做階躍擾動試驗,然后將積分時間Ti 由大到小的變化,直到得到4:1衰減曲線為止.先增加比例帶的原因是加入積分后,系統穩定性,比原來單純比例調節時要降低,增加δ補償加積分作用后而引起得穩定性的降低. 3)積分時間保持不變,加入比例帶,觀察控制過程有無改善,如有改善則繼續調整,直到滿意為止.否則,將原比例帶減小一些,再調整積分時間,力求改善控制過程.如此反復試湊,直到找到滿意的比例帶和積分時間為止. 4)最后再加入微分作用,將微分時間TD 由小到大的調整.觀察每次實驗過程,直到滿意為止. 根據上述思路,寫出代碼如下: - % 主函數
- % 初始化pid參數
- kp=1; ti=1e32; td=0;
- % 定義狀態值,方便debug
- status = 0; % 狀態: 0-未整定,1-整定好p,2-整定好i,3-整定好d,整定完成
- gg0=getLoop(kp, ti, td);
- figure
- step(gg0);
- hold on
- % 整定p, 調整衰減比接近4:1
- while getDelta(kp, ti, td)>4
- % getDelta([kp, ti, td])
- kp = kp*1.01; % kp增大,衰減比減小
- end
- status = 1
- gg1=getLoop(kp, ti, td);
- step(gg1);
- hold on
- % 整定i, 調整衰減比接近4:1
- kp = kp * 0.9; % 減小kp,補償引入積分作用造成的穩定性下降
- while getDelta(kp, ti, td)>4
- % getDelta([kp, ti, td])
- ti = ti*0.9;
- end
- status = 2
- gg2=getLoop(kp, ti, td);
- step(gg2);
- hold on
- % 整定d, 調整衰減比接近4:1
- kp = kp * 0.9; % 減小kp,補償引入積分作用造成的穩定性下降
- td=1e-32;
- while getDelta(kp, ti, td)>4
- % td
- % getDelta(kp, ti, td)
- td = td*1.1;
- end
- status = 3
- gg3=getLoop(kp, ti, td);
- step(gg3);
- legend('intianl respond','respond after setting p','respond after setting i','respond after setting d');
- hold off
- % 返回pid參數為[kp, ti, td]的閉環控制系統的回路方程
- function gg = getLoop(kp, ti, td)
- % 構建方程
- g = tf(25, conv([4 1], [20 1])); % 開環系統
- gc_p = tf(kp, 1); % p控制
- gc_i = tf(kp, [ti 0]); % i控制
- gc_d = tf([kp*td 0], 1); % d控制
- gc = parallel(parallel(gc_p, gc_i), gc_d); % pid控制器
- gg = feedback(series(g, gc), 1); % 總控制系統
- end
- % 計算pid參數為[kp, ti, td]的閉環控制系統的階躍響應衰減比
- function delta = getDelta(kp, ti, td)
- % 得到控制系統階躍響應曲線
- gg = getLoop(kp, ti, td);
- Y = step(gg);
- % 計算衰減比
- V = findpeaks(Y);
- delta = (V(1)-Y(end))/(V(2)-Y(end));
- end
下圖是四步整定之后,閉環控制系統的階躍響應曲線: 由圖中曲線可知,每一步整定完成之后,閉環控制系統的準確性和快速性都略有上升. B 臨界比例帶法(邊界穩定法) 臨界比例帶法的應用較為廣泛,將控制器設置為純比例作用,將系統自動投入運行并將比例帶由大到小進行改變,直到產生等幅振蕩為止,此時控制系統處于邊界穩定狀態,記錄下此刻的比例帶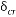 和振蕩周期Tcr ,然后根據下表中的經驗公式進行計算,算出控制器的各個參數. 和振蕩周期Tcr ,然后根據下表中的經驗公式進行計算,算出控制器的各個參數. | | | | | 2 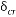 | | | | 2.2 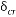 | | | | | | |
具體步驟如下所述: 1) 將控制器的積分時間置于最大,即T1=∞,微分時間TD=0,比例帶δ置于一個較大的數值 2) 將控制系統投入閉環運行,待系統穩定之后,逐步減小比例帶,直到系統出現等幅振蕩,記錄此時的比例帶δcr 和振蕩周期Tcr , 3) 將比例帶δcr 和振蕩周期Tcr 代入上表,計算控制系統各個參數. 根據上述步驟寫出代碼如下: - % 初始pid參數
- kp=1; ti=1e32; td=1e-32;
- % getDelta(kp, ti, td)
- % figure
- % step(getLoop(kp, ti, td))
- history(1, :) = [kp, ti, td];
- % 整定p, 調整衰減比接近1:1
- if getDelta(kp, ti, td) > 1
- while getDelta(kp, ti, td) > 1
- % getDelta([kp, ti, td])
- kp = kp*1.01; % kp增大,衰減比減小
- end
- elseif getDelta(kp, ti, td) < 1
- while getDelta(kp, ti, td) < 1
- % getDelta([kp, ti, td])
- kp = kp*0.99; % kp增大,衰減比減小
- end
- end
- % 計算臨界比例帶
- [Y, T] = step(getLoop(kp, ti, td));
- [pks, locs] = findpeaks(Y);
- tcr = T(locs(2))-T(locs(1));
- % 計算對應的三種控制參數
- % history(1, :) = [kp, ti, td];
- % history(2, :) = [kp/2, 1e32, 1e-32];
- % history(3, :) = [kp/2.2, 0.85*tcr, 1e-32];
- history(4, :) = [kp/1.7, 0.5*tcr, 0.125*tcr];
- % 繪制圖片
- % step(getLoop(history(2, :))); hold on;
- % step(getLoop(history(3, :))); hold on;
- figure
- step(getLoop(history(1, 1),history(1, 2),history(1, 3))); hold on;
- step(getLoop(history(4, 1),history(4, 2),history(4, 3))); hold on;
- legend('initial respond','respond after setting pid')
- function gg = getLoop(kp, ti, td)
- % 構建方程
- g = tf(25, conv([4 1], [20 1])); % 開環系統
- gc_p = tf(kp, 1); % p控制
- gc_i = tf(kp, [ti 0]); % i控制
- gc_d = tf([kp*td 0], 1); % d控制
- gc = parallel(parallel(gc_p, gc_i), gc_d); % pid控制器
- gg = feedback(series(g, gc), 1); % 總控制系統
- end
- % 計算pid參數為[kp, ti, td]的閉環控制系統的階躍響應衰減比
- function delta = getDelta(kp, ti, td)
- % 得到控制系統階躍響應曲線
- gg = getLoop(kp, ti, td);
- Y = step(gg);
- % 計算衰減比
- V = findpeaks(Y);
- delta = (V(1)-Y(end))/(V(2)-Y(end));
- end
對上邊的系統進行整定,我們先將系統比例帶設置由大到小,直到系統等幅振蕩.此時閉環系統階躍響應如下: (num=100;i=0; for sigma=0:1:0 den=[0.00227 100*sigma*0.1 100]; damp(den); sys=tf(num,den); i=i+2; step(sys,0.1) hold on end grid hold off lab1='|?=0'; text(2,8,lab1); ) 因為我們是模擬實際情況查找比例帶,而不是由公式對臨界比例帶進行計算,因此此時系統的衰減比實際上為0.9992,而非1. 代入上邊表格數據時,我發現了一個bug,按照上面表格進行計算,閉環系統采用p控制,pi控制都會導致系統閉環不穩定,而采用pid控制能使系統閉環穩定.整定后的系統的快速性大為改善,然而其準確性略有下降. 臨界比例帶法(邊界穩定法) 如果在生產過程中不允許出現等幅振蕩,則只能退而求其次,采用衰減曲線法.我們只能退而求其次,選擇衰減曲線法,將上邊方法中的等幅振蕩過程改為4:1震蕩過程.其具體步驟與上邊臨界比例帶法類似如下: 1) 設置控制器的積分時間Ti=∞,微分時間TD=0,比例帶δ置于較大的數值 2) 將系統投入閉環運行,待數值穩定之后,做階躍擾動試驗,觀察控制過程,若過渡時間衰減率φ大于要求的數值,則應逐步減小比例帶值,直到系統過度曲線出現φ=0.75或φ=0.9為止.記錄此時的比例帶δs ,在φ=0.75時的衰減曲線上求取衰減周期Ts ,或在φ=0.9的衰減曲線上求取上升時間tr 3) 將比例帶δ\deltaδ和振蕩周期TTT代入上表,計算控制系統各個參數 對于衰減率φ=0.75\varphi=0.75φ=0.75的情況,其實現代碼如下: - % 初始pid參數
- % 初始pid參數
- kp=1; ti=1e32; td=1e-32;
- history(1, :) = [kp, ti, td]; % 記錄初始值
- % 整定p, 調整衰減比接近4:1
- if getDelta(kp, ti, td)>4
- while getDelta(kp, ti, td)>4
- % getDelta([kp, ti, td])
- kp = kp*1.01; % kp增大,衰減比減小
- end
- elseif getDelta(kp, ti, td)<4
- while getDelta(kp, ti, td)<4
- % getDelta([kp, ti, td])
- kp = kp*0.99; % kp增大,衰減比減小
- end
- end
- % 計算臨界比例帶
- [Y, T] = step(getLoop(kp, ti, td));
- [pks, locs] = findpeaks(Y);
- ts = T(locs(2))-T(locs(1));
- % 記錄不同比值
- history(2, :) = [kp, 1e32, 1e-32]; % p控制
- history(3, :) = [kp/1.2, 0.5*ts, 1e-32]; % pi控制
- history(4, :) = [kp/0.8, 0.3*ts, 0.1*ts]; % pid控制
- % 繪圖
- figure
- step(getLoop(history(1, 1),history(1, 2),history(1, 3))); hold on;
- step(getLoop(history(2, 1),history(2, 2),history(2, 3))); hold on;
- step(getLoop(history(3, 1),history(3, 2),history(3, 3))); hold on;
- step(getLoop(history(4, 1),history(4, 2),history(4, 3))); hold on;
- legend('initial respond','respond after setting p','respond after setting pi','respond after setting pid')
- function gg = getLoop(kp, ti, td)
- % 構建方程
- g = tf(25, conv([4 1], [20 1])); % 開環系統
- gc_p = tf(kp, 1); % p控制
- gc_i = tf(kp, [ti 0]); % i控制
- gc_d = tf([kp*td 0], 1); % d控制
- gc = parallel(parallel(gc_p, gc_i), gc_d); % pid控制器
- gg = feedback(series(g, gc), 1); % 總控制系統
- end
- % 計算pid參數為[kp, ti, td]的閉環控制系統的階躍響應衰減比
- function delta = getDelta(kp, ti, td)
- % 得到控制系統階躍響應曲線
- gg = getLoop(kp, ti, td);
- Y = step(gg);
- % 計算衰減比
- V = findpeaks(Y);
- delta = (V(1)-Y(end))/(V(2)-Y(end));
- end
將所得到的結果繪制在坐標軸上,得到圖像如下. 由此可見,在引入積分控制后,控制系統的準確度有所下降.但加入pid控制之后,總體的控制效果比初始情況大為改善. 對于衰減率φ=0.9\varphi=0.9φ=0.9的情況下,其實現代碼如下: - % 初始pid參數
- kp=1; ti=1e32; td=1e-32;
- history(1, :) = [kp, ti, td]; % 記錄初始值
- % 整定p, 調整衰減比接近4:1
- if getDelta(kp, ti, td)>10
- while getDelta(kp, ti, td)>10
- % getDelta([kp, ti, td])
- kp = kp*1.01; % kp增大,衰減比減小
- end
- elseif getDelta(kp, ti, td)<10
- while getDelta(kp, ti, td)<10
- % getDelta([kp, ti, td])
- kp = kp*0.99; % kp增大,衰減比減小
- end
- end
- % 計算臨界比例帶
- [Y, T] = step(getLoop(kp, ti, td));
- [pks, locs] = findpeaks(Y);
- ts = T(locs(2))-T(locs(1));
- % 記錄不同比值
- history(2, :) = [kp, 1e32, 1e-32]; % p控制
- history(3, :) = [kp/1.2, 0.5*ts, 1e-32]; % pi控制
- history(4, :) = [kp/0.8, 0.3*ts, 0.1*ts]; % pid控制
- % 繪圖
- figure
- step(getLoop(history(1, 1),history(1, 2),history(1, 3))); hold on;
- step(getLoop(history(2, 1),history(2, 2),history(2, 3))); hold on;
- step(getLoop(history(3, 1),history(3, 2),history(3, 3))); hold on;
- step(getLoop(history(4, 1),history(4, 2),history(4, 3))); hold on;
- legend('initial respond','respond after setting p','respond after setting pi','respond after setting pid')
- function gg = getLoop(kp, ti, td)
- % 構建方程
- g = tf(25, conv([4 1], [20 1])); % 開環系統
- gc_p = tf(kp, 1); % p控制
- gc_i = tf(kp, [ti 0]); % i控制
- gc_d = tf([kp*td 0], 1); % d控制
- gc = parallel(parallel(gc_p, gc_i), gc_d); % pid控制器
- gg = feedback(series(g, gc), 1); % 總控制系統
- end
- % 計算pid參數為[kp, ti, td]的閉環控制系統的階躍響應衰減比
- function delta = getDelta(kp, ti, td)
- % 得到控制系統階躍響應曲線
- gg = getLoop(kp, ti, td);
- Y = step(gg);
- % 計算衰減比
- V = findpeaks(Y);
- delta = (V(1)-Y(end))/(V(2)-Y(end));
- end
將所得到的結果繪制在坐標軸上,得到圖像如下. 我們得到的結果與衰減率φ=0.75\varphi=0.75φ=0.75的情況類似,得到結論: 在引入積分控制后,控制系統的準確度有所下降.但加入pid控制之后,總體的控制效果比初始情況大為改善. D響應曲線法(動態特性參數法) 前面三種方法都是針對系統的閉環特性進行整定,而響應曲線法是根據系統的開環狀態下,通過階躍擾動試驗得到pid控制的各種參數. 下面是響應曲線法的執行步驟: 1) 給對象一個階躍輸入,記錄其輸出. 2) 判斷對象是否有自平衡能力: 2.1)若對象由自平衡能力,過響應曲線拐點P作切線交穩態值漸近線y(∞)A點,交時間軸于C點,過直線段上任意一點A作時間垂線并交于B點,則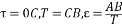 ? ? 2.2) 若對象無自平衡能力,做響應曲線漸近線交時間軸于C,過直線段上任一點A做時間垂線并交于B,則 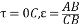 ? ? 3) 查下表,確定控制器的整定參數 代碼如下: % 初始化開環系統 g = tf(25, [80 24 1]); [Y, T] = step(g); % 尋找拐點P及其斜率 [val, minindex] = min(diff(Y, 2)); PX = T(minindex); PY = val; k = (Y(minindex+1) - Y(minindex))/(T(minindex+1) - T(minindex)); % 找到點C CX = PX - PY/k; CY = 0; AY = Y(end); AX = PX + (AY - PY) / k; % 計算 tau,epsilon tau = CX; epsilon = AY / (AX - CX); % 記錄pid參數 history(1, :) = [1, 1e32, 1e-32]; % 不加pid控制 history(2, :) = [epsilon*tau, 1e32, 1e-32]; % p控制 history(3, :) = [epsilon*tau, 3.3*tau, 1e-32]; % pi控制 history(4, :) = [epsilon*tau, 2*tau, 0.5*tau]; % pid控制 figure step(getLoop(history(1, 1),history(1, 2),history(1, 3))); hold on; step(getLoop(history(2, 1),history(2, 2),history(2, 3))); hold on; step(getLoop(history(3, 1),history(3, 2),history(3, 3))); hold on; step(getLoop(history(4, 1),history(4, 2),history(4, 3))); hold on; legend('initial respond','respond after setting p','respond after setting pi','respond after setting pid'); function gg = getLoop(kp, ti, td) % 構建方程 g = tf(25, conv([4 1], [20 1])); % 開環系統 gc_p = tf(kp, 1); % p控制 gc_i = tf(kp, [ti 0]); % i控制 gc_d = tf([kp*td 0], 1); % d控制 gc = parallel(parallel(gc_p, gc_i), gc_d); % pid控制器 gg = feedback(series(g, gc), 1); % 總控制系統 end % 計算pid參數為[kp, ti, td]的閉環控制系統的階躍響應衰減比 function delta = getDelta(kp, ti, td) % 得到控制系統階躍響應曲線 gg = getLoop(kp, ti, td); Y = step(gg); % 計算衰減比 V = findpeaks(Y); delta = (V(1)-Y(end))/(V(2)-Y(end)); end 執行上述代碼,我們得到結果如下: 由上圖可見,p控制,pi控制的效果并不是很好,但是引入pid控制之后,系統的動態特性大為改善,這時因為我們所選的被控對象的慣性較大. 各種整定方法的總結與比較 下面對四種工程整定方法做出總結并加以比較,在本次實驗中,我們共使用了四種整定方法: 1) 經驗法: 花費時間長,難以總結出一般規律 2) 臨界比例帶法: 方法簡單且易用,但是實際情況下難以實現,且整定后的系統容易發生不穩定振蕩; 3) 衰減曲線法: 衰減曲線法作為臨界比例帶法的改進,方法較簡單,且在實際情況下有條件實現,但是在實際整定過程中難以實現完美的4:1衰減模型; 4) 響應曲線法: 簡單省時,可以直接通過開環特性整定閉環系統,但是計算誤差較大. 在實際的編程中,我們發現各種程序的運行效率由高到低如下: 響應曲線法>臨界比例帶法>衰減曲線法>經驗法.經驗法中因為需要大量試湊,所以程序的運行時間實在太長,且我這個小破電腦還動不動死機; 在臨界比例帶正定方法的實現過程中,出現了系統不穩定,因此我們在這里對pid控制方法的穩定想加以總結: 5) P控制: 比例控制的放大系數Kp大小應適當. 5.1) 若Kp 過小,則控制通道難以屏蔽干擾通道的效果,使得總體上的控制效果較差. 5.2) 若Kp 過大,則系統容易出現不穩定震蕩; 6) PI控制: 引入積分控制,控制系統的穩定性會下降.因此我們在試湊法中整定Ti 之前要適當增加比例帶δ; 7) PID控制: 引入微分控制后,系統的穩定性增加,因此可以適當降低比例帶δ。
以上的Word格式文檔51黑下載地址:
 單回路參數pid整定.docx
(357.69 KB, 下載次數: 28)
單回路參數pid整定.docx
(357.69 KB, 下載次數: 28)
2020-6-19 10:26 上傳
點擊文件名下載附件
下載積分: 黑幣 -5
|