|
感謝匿名的開源分享,感謝群友的熱心幫助。 說什么四元數完全解析其實都是前輩們的解析,小弟真心是一個搬磚的,搬得不好希望大神們給以批評和指正,在此謝過了。因為本人是小菜鳥一枚,對,最菜的那種菜鳥······所以對四元數求解姿態角這么一個在大神眼里簡單的算法,小弟我還是費了很大勁才稍微理解了那么一點點,小弟搬磚整理時也是基于小弟的理解和智商的,有些太基礎,有些可能錯了,大牛們發現了再罵過我后希望能夠給與指正哈。 好,廢話到此為止,開始說主體。四元數和姿態角怎么說呢?先得給和我一樣的小菜鳥們理一理思路,小鳥我在此畫了一個“思維導圖”(我承認我畫的丑),四元數解算姿態首先分為兩部分理解:第一部分先理解什么是四元數,四元數與姿態角間的關系;第二部分要理解怎么由慣性單元測出的加速度和角速度求出四元數,再由四元數求出歐拉角。 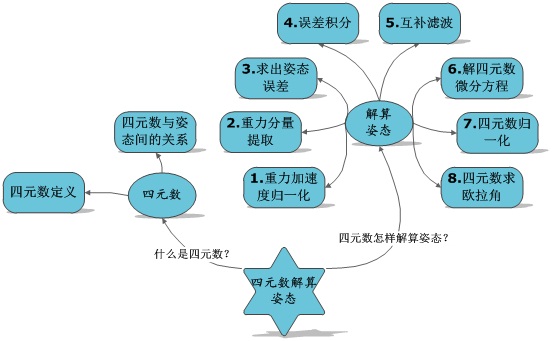
圖1 渣渣思維導圖 在講解什么是四元數時,小弟的思維是順著說的,先由四元數的定義說起,說到四元數與姿態角間的關系。但在講解姿態解算時,小弟的思維是逆向的,就是反推回來的,從歐拉角一步步反推回到慣性器件的測量數據,這樣逆向說是因為便于理解,因為實際在工程應用時和理論推導有很大差別。 實際應用時正確的求解順序應該為圖1中序號順序,即1->2->3->……. 但在筆者講解姿態求解時思路是如圖2的。 
圖2 逆向講解思路 大家在看四元數時最好結合著代碼一塊看,小弟看的是匿名四軸的代碼,感覺寫的非常好也非常清晰,粘出來大家一塊觀摩。紅色部分是核心代碼,總共分為八個步驟,和圖1中的八個步驟是一一對應的。講解介紹時也是和代碼對比起來講解的。代碼可以去匿名官網上下載,都是開源的,不是小弟的,所以小弟不方便加在附件中。 //四元數更新姿態 #define Kp 2.0f //加速度權重,越大則向加速度測量值收斂越快 #define Ki 0.001f //誤差積分增益 void ANO_IMU::Quaternion_CF(Vector3f gyro,Vector3f acc, float deltaT) { Vector3f V_gravity, V_error, V_error_I; //1.重力加速度歸一化 acc.normalize(); //2.提取四元數的等效余弦矩陣中的重力分量 Q.vector_gravity(V_gravity); //3.向量叉積得出姿態誤差 V_error = acc % V_gravity; //4.對誤差進行積分 V_error_I += V_error * Ki; //5.互補濾波,姿態誤差補償到角速度上,修正角速度積分漂移 Gyro += V_error * Kp + V_error_I; //6.一階龍格庫塔法更新四元數 Q.Runge_Kutta_1st(Gyro, deltaT); //7.四元數歸一化 Q.normalize(); //8.四元數轉歐拉角 Q.to_euler(&angle.x, &angle.y, &angle.z); } |
好的,下面搬磚開始!。。。。。。。。嘿咻嘿咻!!!!
一. 什么是四元數?關于四元數的定義摘自秦永元的《慣性導航》,里面有非常好的講解,大家可以直接看緒論和第九章就可以。下面我粘貼了部分原文,粘貼的比較多比較詳細,應為本人比較笨還愛較真,所以按本人的風格就要詳盡一點,大牛們都可以自動忽略。 四元數定義、表達方式及運算方法——摘自《慣性導航》-秦永元P289-292
|
好,關于四元數定義就搬這么多,其他的大家去附件下載《慣性導航》的pdf自己看吧。 下面開始搬四元數與姿態解算關系的。。。。。。嘿咻嘿咻~~~~
二、四元數與姿態陣間的關系從上面我們知道了四元數的定義,可這四個數和我們要求的三個姿態角有什么關系呢?下面是詳細的推導,同樣摘自《慣性導航》-秦永元P292-297。 四元數與姿態陣間的關系——摘自《慣性導航》-秦永元P292-297
|
呃,粘了這么多其實就是為了想知道推導過程小伙伴好理解,真正有用的就是(9.2.34)這個公式。▲這個公式把四元數轉換成了方向余弦矩陣中的幾個元素,再用這幾個元素轉換為歐拉角。就求解除了姿態! 
先從四元數q0~q3轉成方向余弦矩陣: 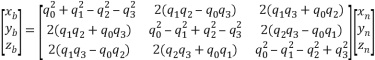
再從方向余弦矩陣轉換為歐拉角: 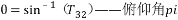
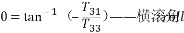
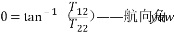
好的,公式原理都講清楚了,下面來看一下匿名的代碼: //四元數轉歐拉角,這里四元數是q1~q4 和公式里q0~q3相對應。 void Quaternion::to_euler(float *roll, float *pitch, float *yaw) { if (roll) { *roll = degrees(atan2f(2.0f*(q1*q2 + q3*q4),1 - 2.0f*(q2*q2 + q3*q3))); //*roll = degrees(atan2f(-2.0f*(q2*q4 - q1*q3),1 - 2.0f*(q2*q2 + q3*q3))); } if (pitch) { // 使用safe_asin()來處理pitch接近90/-90時的奇點 *pitch = degrees(safe_asin(2.0f*(q1*q3 - q2*q4))); //*pitch = degrees(safe_asin(2.0f*(q3*q4 + q1*q2))); } if (yaw) { *yaw = degrees(atan2f(2.0f*(q2*q3 - q1*q4), 2.0f*(q1*q1 + q2*q2) - 1)); //*yaw = degrees(atan2f(2.0f*(q2*q3 - q1*q4), 2.0f*(q1*q1 + q3*q3) - 1)); } } |
對比余弦矩陣轉換為歐拉角的公式很容易理解了吧,注意一下,紅色是匿名原版的代碼,和公式還是有出入的,自己細心觀察一下吧。被注釋了的黑色代碼是我根據上面的公式寫的。但黑色的求解出來的歐拉角反映出來的姿態是不對的,具體表現為俯仰(pitch)和橫滾(roll)是相反的,為啥根據公式寫的是不對的?群里的小伙伴給與了我熱心的解答。 這個錯誤主要是由于方向余弦矩陣的旋轉順序不一樣,也就是公式(9.2.39)不一樣,這是由于旋轉的先后順序不同引起的,具體大家參考《慣性導航》緒論來看就能明白,因為這一點小弟還有點混亂,就點到這為止。 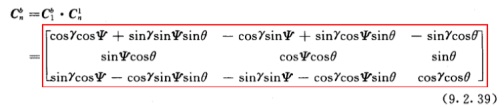
以上就是四元數求解歐拉角的方法。通過公式可以看到,要求歐拉角需要求得四元數的方向余弦矩陣;要求得四元數方向余弦矩陣,需要求得四元數q0~q3,那么如何求得q0~q3?接下來詳細介紹。 三、四元數微分及龍格庫塔求Q0~Q3首先我們先來看一下在程序里如何求解的q0~q3: //一階龍格庫塔法更新四元數 void Quaternion::Runge_Kutta_1st(Vector3f &g, float deltaT) { q1 += 0.5 * (-q2*g.x - q3*g.y - q4*g.z)* deltaT; q2 += 0.5 * (q1*g.x + q3*g.z - q4*g.y)* deltaT; q3 += 0.5 * (q1*g.y - q2*g.z + q4*g.x)* deltaT; q4 += 0.5 * (q1*g.z + q2*g.y - q3*g.x)* deltaT; } |
這就是一階龍格庫塔法求解q的微分方程,傳入參數只需要這個周期的角速度g.x、g.y、g.z和周期時間deltaT。下面一張是從某位大神的貼吧上盜的圖,描繪的是一階龍格庫塔的計算式。 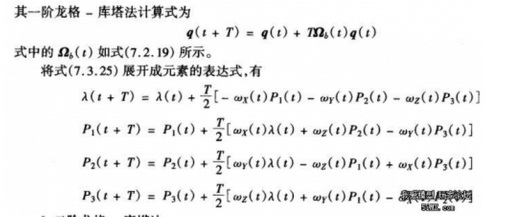
相信很多人和我一樣,單看上圖很難理解其中的意思和其由來,于是我又找了很多帖子,感謝前人做出的貢獻,小弟在這里再次整理大神的四元數微分方程推導公式,便于大家理解。摘自附件中《推導_四元數.pdf》 雖然在下也不是很懂,不過粘出來還是能起到理解的作用,這樣大家就不會覺得這是憑空變出來的,本人數學功底薄弱,沒有對推導進行過驗證,如果有不對的地方歡迎指正。 接著使用一階龍格庫塔(Runge-Kutta)發求出q0~q3,這一點很多人不知道一階龍格庫塔怎么推導的,下面也是這位網友的推導,大家參考著理解吧。 這里的角速度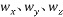 是由捷聯陀螺的輸出(對機械轉子陀螺必須經過誤差補償,將在下面介紹)。 是由捷聯陀螺的輸出(對機械轉子陀螺必須經過誤差補償,將在下面介紹)。 對比著匿名四軸的代碼看一看(g.x、g.y、g.z是捷聯陀螺的輸出),代碼的意思就比較清楚了。在往上一步步推,我們就要求陀螺輸出了,并且還要對數據進行互補濾波處理。 四、慣性單元測量值融合這部分看似很簡單,但是也有讓筆者難以理解的地方,希望后人能補充修正進行更好的講解。有了上一步的龍格庫塔方程,我們現在需要的就是角速度的測量值。 在四軸上安裝陀螺儀,可以測量四軸傾斜的角速度,由于陀螺儀輸出的是四軸的角速度,不會受到四軸振動影響。因此該信號中噪聲很小。四軸的角度又是通過對角速度積分而得,這可進一步平滑信號,從而使得角度信號更加穩定。因此四軸控制所需要的角度和角速度可以使用陀螺儀所得到的信號。由于從陀螺儀的角速度獲得角度信息,需要經過積分運算。如果角速度信號存在微小的偏差,經過積分運算之后,變化形成積累誤差。這個誤差會隨著時間延長逐步增加,最終導致電路飽和,無法形成正確的角度信號。 如何消除這個累積誤差呢?可以通過上面的加速度傳感器獲得的角度信息對此進行校正。利用加速度計所獲得的角度信息 θg 與陀螺儀積分后的角度θ 進行比較,將比較的誤差信號經過比例Tg 放大之后與陀螺儀輸出的角速度信號疊加之后再進行積分。對于加速度計給定的角度θg ,經過比例、積分環節之后產生的角度θ必然最終等于θg 。由于加速度計獲得的角度信息不會存在積累誤差,所以最終將輸出角度θ中的積累誤差消除了。加速度計所產生的角度信息θg 中會疊加很強的有四軸運動加速度噪聲信號。為了避免該信號對于角度θ 的影響,因此比例系數 Tg 應該非常小。這樣,加速度的噪聲信號經過比例、積分后,在輸出角度信息中就會非常小了。由于存在積分環節,所以無論比例Tg多么小,最終輸出角度θ必然與加速度計測量的角度θg相等,只是這個調節過程會隨著Tg 的減小而延長。 先把這個過程的代碼粘出來,看著代碼一步步理解: #define Kp 2.0f //加速度權重,越大則向加速度測量值收斂越快 #define Ki 0.001f //誤差積分增益 //1.重力加速度歸一化 acc.normalize(); //2.提取四元數的等效余弦矩陣中的重力分量 Q.vector_gravity(V_gravity); //3.向量叉積得出姿態誤差 V_error = acc % V_gravity; //4.對誤差進行積分 V_error_I += V_error * Ki; //5.互補濾波,姿態誤差補償到角速度上,修正角速度積分漂移 Gyro += V_error * Kp + V_error_I; |
1.重力加速度歸一化:加速度計數據歸一化,把加速度計的三維向量轉換為單位向量, 因為是單位矢量到參考性的投影,所以要把加速度計數據單位化,其實歸一化改變的只是這三個向量的長度,也就是只改變了相同的倍數,方向并沒有改變,也是為了與單位四元數對應。 2.提取四元數的等效余弦矩陣中的重力分量: // 返回該四元數的等效余弦矩陣中的重力分量 void Quaternion::vector_gravity(Vector3f &v) { v.x = 2*(q2*q4 - q1*q3); v.y = 2*(q1*q2 + q3*q4); v.z = 1-2*(q2*q2 + q3*q3); } |
將當前姿態的重力在三個軸上的分量分離出來,把四元數換算成方向余弦中的第三行的三個元素,根據余弦矩陣和歐拉角的定義,就是地理坐標系(參考坐標系)的Z軸的重力向量。當我讀完這句話腦子挺懵的,鬧不明白啊,于是又找到了下面的資料,可以進行解釋了。 別忘了這是個正交矩陣哦!這樣就知道代碼怎么來的了吧?好繼續。 3.向量叉積得出姿態誤差: 哎呀,又來棘手問題了,這個我也不太明白怎么講啊,還是把大神的講解粘過來吧,大家看看是不是這么回事: acc是機體坐標參照系上,加速度計測出來的重力向量,也就是實際測出來的重力向量。 acc是測量得到的重力向量,V_gravity是陀螺積分后的姿態來推算出的重力向量,它們都是機體坐標參照系上的重力向量。 那它們之間的誤差向量,就是陀螺積分后的姿態和加計測出來的姿態之間的誤差。 向量間的誤差,可以用向量叉積(也叫向量外積、叉乘)來表示,V_error就是兩個重力向量的叉積。 這個叉積向量仍舊是位于機體坐標系上的,而陀螺積分誤差也是在機體坐標系,而且叉積的大小與陀螺積分誤差成正比,正好拿來糾正陀螺。(你可以自己拿東西想象一下)由于陀螺是對機體直接積分,所以對陀螺的糾正量會直接體現在對機體坐標系的糾正。 |
看了上面的話,小弟一直對這個誤差向量感到莫名其妙,后來又找到大神的一下一段話: 這里誤差沒說清楚,不是指向量差。這個叉積誤差是指將帶有誤差的加計向量轉動到與重力向量重合,需要繞什么軸,轉多少角度。逆向推理一下,這個叉積在機體三軸上的投影,就是加計和重力之間的角度誤差。也就是說,如果陀螺按這個叉積誤差的軸,轉動叉積誤差的角度(也就是轉動三軸投影的角度)那就能把加計和重力向量的誤差消除掉。(具體可看向量叉積的定義)如果完全按叉積誤差轉過去,那就是完全信任加計。如果一點也不轉,那就是完全信任陀螺。那么把這個叉積的三軸乘以x%,加到陀螺的積分角度上去,就是這個x%互補系數的互補算法了。 |
這個看了好像終于理解點了,再看下代碼: //3.向量叉積得出姿態誤差 V_error = acc % V_gravity; |
這里“ % ”已經重定義為叉乘的算法了。 4.對誤差進行積分: 積分求誤差,關于當前姿態分離出的重力分量,與當前加速度計測得的重力分量的差值進行積分消除誤差 V_error_I += V_error * Ki; |
5.互補濾波,姿態誤差補償到角速度上,修正角速度積分漂移 系數不停地被陀螺積分更新,也不停地被誤差修正,它和公式所代表的姿態也在不斷更新。 將積分誤差反饋到陀螺儀上,修正陀螺儀的值。將該誤差V_error輸入 PI 控制器后與本次姿態更新周期中陀螺儀測得的角速度相加,最終得到一個修正的角速度值,將其輸入四元數微分方程,更新四元數。 Gyro += V_error * Kp + V_error_I; |
Gyro就是得到的修正角速度值,可以用于求解四元數q0~q3了。 到這里回顧一下八個步驟還漏了一個第七步: 7.四元數歸一化: 規范化四元數作用: 1.表征旋轉的四元數應該是規范化的四元數,但是由于計算誤差等因素,計算過程中四元數會逐漸失去規范化特性,因此必須對四元數做規范化處理。 2.意義在于單位化四元數在空間旋轉時是不會拉伸的,僅有旋轉角度.這類似與線性代數里面的正交變換。 3.由于誤差的引入,使得計算的變換四元數的模不再等于1,變換四元數失去規范性,因此再次更新四元數。 計算歐拉角時候必須要對四元數歸一化處理。
呃,關于四元數求解姿態的磚好像搬完了。為什么要用四元數法求解姿態呢?再搬一點關于歐拉角法和旋轉矢量法的介紹的。
搬磚搬得好累啊,不過搬得差不多了,感覺挺亂的?呃,主要是由于比較多吧,那我再串一遍?拉倒吧,你看得都累,我寫著不累?沒鬧明白再自己串一遍吧,相信第二遍就能明白了。 哎~對于我這樣的渣渣而言也就能理解到這一步了,這也是我好幾天的心血整理了一下,也許有和我一樣的菜鳥呢,對他們也許能有點幫助,做得不好希望大神們能耐心給與指正,而不是嗤之以鼻,或者噴我一頓就走。。。畢竟整理了兩天呢(我還以為一中午就能搞定呢)。渣渣的學習之路也是挺不容易的,因為基礎渣渣,學校渣渣,所以難以得到有效地幫助和指導,有時在群里尋求幫助,無聊的群友會告訴你看書去,呵呵。。。我也知道看書啊。。。哪怕你能告訴我我的問題在那本書的那部分能有相似吧?一句看書去,上網查啊,等于沒回答,如果一直這樣自己看下去可能半年也解決不了,因為渣渣的學習環境是有局限性的。 不過好在有更多很熱心的群友能提供給我幫助,把他們收集的好貼發給我,或者干脆手寫一個公式推導,一個電路圖,然后拍照發給我,還有的幫我下載照片,分類命名給我,艾瑪!熱淚盈眶啊有木有!!!再次感謝這些熱心幫助我的小伙伴@奇點,@杜掌柜,@廉價物品,@忘記名字的小伙伴······ 下面附上被我搬磚的幾個好貼,謝謝大神們的樂于分享: |