前段時(shí)間的RoboMaster機(jī)器人大賽相信不少人都進(jìn)行了或多或少的了解，不過(guò)這種機(jī)器人的輪胎似乎長(zhǎng)得有點(diǎn)奇怪。
這種輪胎不會(huì)像汽車那樣轉(zhuǎn)向卻能夠讓賽場(chǎng)上的機(jī)器人朝著各個(gè)方向移動(dòng)。今天我們就來(lái)說(shuō)說(shuō)這種讓神奇的“麥克納姆輪”。
其實(shí)這篇文章是兩年前一位知乎網(wǎng)友“科長(zhǎng)”發(fā)表的，原文名稱是“【學(xué)渣的自我修養(yǎng)】麥克納姆輪淺談”，而且還做了一段小視頻，只是在視頻中這麥克納姆輪老師掉鏈子。下面就讓我們來(lái)看看這位“科長(zhǎng)”是科普這“麥克納姆輪”的……
先看視頻：
什么是麥克納姆輪
在競(jìng)賽機(jī)器人和特殊工種機(jī)器人中，全向移動(dòng)經(jīng)常是一個(gè)必需的功能。「全向移動(dòng)」意味著可以在平面內(nèi)做出任意方向平移同時(shí)自轉(zhuǎn)的動(dòng)作。為了實(shí)現(xiàn)全向移動(dòng)，一般機(jī)器人會(huì)使用「全向輪」（Omni Wheel）或「麥克納姆輪」（Mecanum Wheel）這兩種特殊輪子。
全向輪
麥克納姆輪
全向輪與麥克納姆輪的共同點(diǎn)在于他們都由兩大部分組成：輪轂和輥?zhàn)樱╮oller）。輪轂是整個(gè)輪子的主體支架，輥?zhàn)觿t是安裝在輪轂上的鼓狀物。全向輪的 輪轂軸與輥?zhàn)愚D(zhuǎn)軸相互垂直，而麥克納姆輪的輪轂軸與輥?zhàn)愚D(zhuǎn)軸呈 45° 角。理論上，這個(gè)夾角可以是任意值，根據(jù)不同的夾角可以制作出不同的輪子，但最常用的還是這兩種。
全向輪與麥克納姆輪（以下簡(jiǎn)稱「麥輪」）在結(jié)構(gòu)、力學(xué)特性、運(yùn)動(dòng)學(xué)特性上都有差異，其本質(zhì)原因是輪轂軸與輥?zhàn)愚D(zhuǎn)軸的角度不同。經(jīng)過(guò)分析，二者的運(yùn)動(dòng)學(xué)和力學(xué)特性區(qū)別可以通過(guò)上面表格來(lái)體現(xiàn)。
計(jì)算過(guò)程如上圖所示（供參考），學(xué)霸可點(diǎn)開(kāi)大圖驗(yàn)算。
近 年來(lái)，麥輪的應(yīng)用逐漸增多，特別是在 Robocon、FRC 等機(jī)器人賽事上。這是因?yàn)辂溈思{姆輪可以像傳統(tǒng)輪子一樣，安裝在相互平行的軸上。而若想使用全向輪完成類似的功能，幾個(gè)輪轂軸之間的角度就必須是 60°，90° 或 120° 等角度，這樣的角度生產(chǎn)和制造起來(lái)比較麻煩。
 所以許多工業(yè)全向移動(dòng)平臺(tái)都是使用麥克納姆輪而不是全向輪，比如這個(gè)國(guó)產(chǎn)的叉車： 全向移動(dòng)平臺(tái) 麥克納姆輪叉車 美科斯叉車。
另外一個(gè)原因，可能是麥輪的造型比全向輪要酷炫得多，看起來(lái)有一種不明覺(jué)厲的感覺(jué)……
 的確，第一次看到麥輪運(yùn)轉(zhuǎn)起來(lái)，不少人都會(huì)驚嘆。以下視頻直觀地說(shuō)明了麥輪底盤在平移和旋轉(zhuǎn)時(shí)的輪子旋轉(zhuǎn)方向。
麥克納姆輪工作原理
麥輪的安裝方法
麥輪一般是四個(gè)一組使用，兩個(gè)左旋輪，兩個(gè)右旋輪。左旋輪和右旋輪呈手性對(duì)稱，區(qū)別如下圖。 安 裝方式有多種，主要分為：X-正方形（X-square）、X-長(zhǎng)方形（X-rectangle）、O-正方形（O-square）、O-長(zhǎng)方形（O- rectangle）。其中 X 和 O 表示的是與四個(gè)輪子地面接觸的輥?zhàn)铀纬傻膱D形；正方形與長(zhǎng)方形指的是四個(gè)輪子與地面接觸點(diǎn)所圍成的形狀。
 X-正方形：輪子轉(zhuǎn)動(dòng)產(chǎn)生的力矩會(huì)經(jīng)過(guò)同一個(gè)點(diǎn)，所以 yaw 軸無(wú)法主動(dòng)旋轉(zhuǎn)，也無(wú)法主動(dòng)保持 yaw 軸的角度。一般幾乎不會(huì)使用這種安裝方式。
X-長(zhǎng)方形：輪子轉(zhuǎn)動(dòng)可以產(chǎn)生 yaw 軸轉(zhuǎn)動(dòng)力矩，但轉(zhuǎn)動(dòng)力矩的力臂一般會(huì)比較短。這種安裝方式也不多見(jiàn)。
O-正方形：四個(gè)輪子位于正方形的四個(gè)頂點(diǎn)，平移和旋轉(zhuǎn)都沒(méi)有任何問(wèn)題。受限于機(jī)器人底盤的形狀、尺寸等因素，這種安裝方式雖然理想，但可遇而不可求。
O-長(zhǎng)方形：輪子轉(zhuǎn)動(dòng)可以產(chǎn)生 yaw 軸轉(zhuǎn)動(dòng)力矩，而且轉(zhuǎn)動(dòng)力矩的力臂也比較長(zhǎng)。是最常見(jiàn)的安裝方式。
麥輪底盤的正逆運(yùn)動(dòng)學(xué)模型
以O(shè)-長(zhǎng)方形的安裝方式為例，四個(gè)輪子的著地點(diǎn)形成一個(gè)矩形。正運(yùn)動(dòng)學(xué)模型（forward kinematic model）將得到一系列公式，讓我們可以通過(guò)四個(gè)輪子的速度，計(jì)算出底盤的運(yùn)動(dòng)狀態(tài)；而逆運(yùn)動(dòng)學(xué)模型（inverse kinematic model）得到的公式則是可以根據(jù)底盤的運(yùn)動(dòng)狀態(tài)解算出四個(gè)輪子的速度。需要注意的是，底盤的運(yùn)動(dòng)可以用三個(gè)獨(dú)立變量來(lái)描述：X軸平動(dòng)、Y軸平動(dòng)、 yaw 軸自轉(zhuǎn)；而四個(gè)麥輪的速度也是由四個(gè)獨(dú)立的電機(jī)提供的。所以四個(gè)麥輪的合理速度是存在某種約束關(guān)系的，逆運(yùn)動(dòng)學(xué)可以得到唯一解，而正運(yùn)動(dòng)學(xué)中不符合這個(gè)約束關(guān)系的方程將無(wú)解。
先試圖構(gòu)建逆運(yùn)動(dòng)學(xué)模型，由于麥輪底盤的數(shù)學(xué)模型比較復(fù)雜，我們?cè)诖朔炙牟竭M(jìn)行：
①將底盤的運(yùn)動(dòng)分解為三個(gè)獨(dú)立變量來(lái)描述；
②根據(jù)第一步的結(jié)果，計(jì)算出每個(gè)輪子軸心位置的速度；
③根據(jù)第二步的結(jié)果，計(jì)算出每個(gè)輪子與地面接觸的輥?zhàn)拥乃俣龋?br />
④根據(jù)第三部的結(jié)果，計(jì)算出輪子的真實(shí)轉(zhuǎn)速。
一、底盤運(yùn)動(dòng)的分解
我們知道，剛體在平面內(nèi)的運(yùn)動(dòng)可以分解為三個(gè)獨(dú)立分量：X軸平動(dòng)、Y軸平動(dòng)、yaw 軸自轉(zhuǎn)。如下圖所示，底盤的運(yùn)動(dòng)也可以分解為三個(gè)量：
 表示 X 軸運(yùn)動(dòng)的速度，即左右方向，定義向右為正；
 表示 Y 軸運(yùn)動(dòng)的速度，即前后方向，定義向前為正；
 右表示 yaw 軸自轉(zhuǎn)的角速度，定義逆時(shí)針為正。
 以上三個(gè)量一般都視為四個(gè)輪子的幾何中心（矩形的對(duì)角線交點(diǎn)）的速度。
二、計(jì)算出輪子軸心位置的速度
定義：
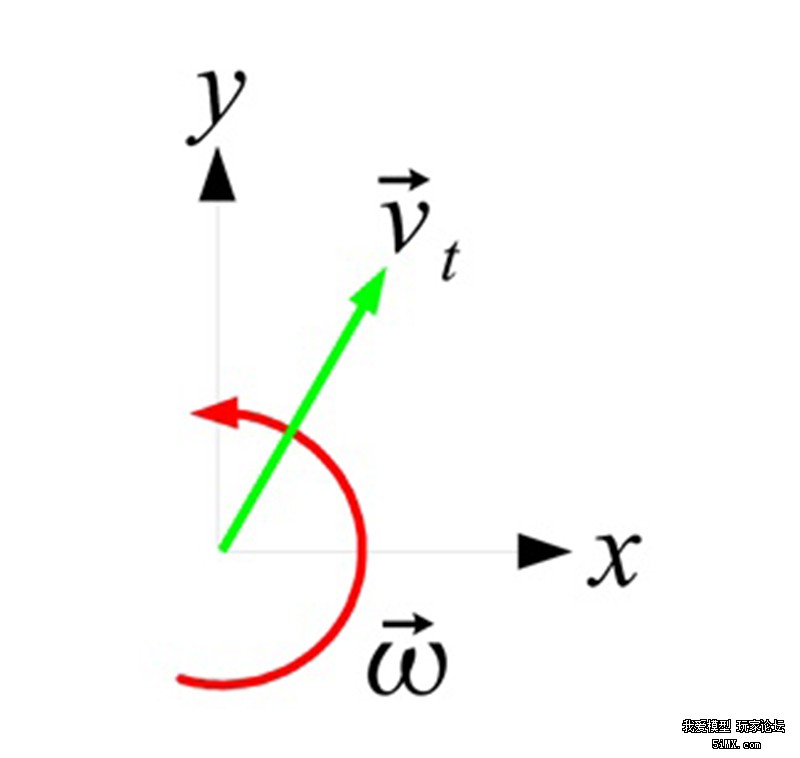
 為從幾何中心指向輪子軸心的矢量；
 為輪子軸心的運(yùn)動(dòng)速度矢量；
 為輪子軸心沿垂直于 \vec{r} 的方向（即切線方向）的速度分量；
那么可以計(jì)算出：
分別計(jì)算 X、Y 軸的分量為：
同理可以算出其他三個(gè)輪子軸心的速度。
三、計(jì)算輥?zhàn)拥乃俣?/font>
根據(jù)輪子軸心的速度，可以分解出沿輥?zhàn)臃较虻乃俣?img id="aimg_cW96Z" onclick="zoom(this, this.src, 0, 0, 0)" class="zoom" width="19" height="31" src="http://c.51hei.com/a/huq/a/a/0/17_files/equation_014.svg" border="0" alt="" />和垂直于輥?zhàn)臃较虻乃俣?img id="aimg_ngW9G" onclick="zoom(this, this.src, 0, 0, 0)" class="zoom" width="21" height="27" src="http://c.51hei.com/a/huq/a/a/0/17_files/equation_005.svg" border="0" alt="" />。其中 是可以無(wú)視的（思考題：為什么垂直方向的速度可以無(wú)視？），而
其中 是沿輥?zhàn)臃较虻膯挝皇噶俊?/font>
四、計(jì)算輪子的速度
從輥?zhàn)铀俣鹊捷喿愚D(zhuǎn)速的計(jì)算比較簡(jiǎn)單：
根據(jù)上圖所示的 a 和 b 的定義，有
結(jié)合以上四個(gè)步驟，可以根據(jù)底盤運(yùn)動(dòng)狀態(tài)解算出四個(gè)輪子的轉(zhuǎn)速：
以上方程組就是O-長(zhǎng)方形麥輪底盤的逆運(yùn)動(dòng)學(xué)模型，而正運(yùn)動(dòng)學(xué)模型可以直接根據(jù)逆運(yùn)動(dòng)學(xué)模型中的三個(gè)方程解出來(lái)，此處不再贅述。
另一種計(jì)算方式
「?jìng)鹘y(tǒng)」的推導(dǎo)過(guò)程雖然嚴(yán)謹(jǐn)，但還是比較繁瑣的。這里介紹一種簡(jiǎn)單的逆運(yùn)動(dòng)學(xué)計(jì)算方式。
我們知道，全向移動(dòng)底盤是一個(gè)純線性系統(tǒng)，而剛體運(yùn)動(dòng)又可以線性分解為三個(gè)分量。那么只需要計(jì)算出麥輪底盤在「沿X軸平移」、「沿Y軸平移」、「繞幾何中 心自轉(zhuǎn)」時(shí)，四個(gè)輪子的速度，就可以通過(guò)簡(jiǎn)單的加法，計(jì)算出這三種簡(jiǎn)單運(yùn)動(dòng)所合成的「平動(dòng)+旋轉(zhuǎn)」運(yùn)動(dòng)時(shí)所需要的四個(gè)輪子的轉(zhuǎn)速。而這三種簡(jiǎn)單運(yùn)動(dòng)時(shí)，四 個(gè)輪子的速度可以通過(guò)簡(jiǎn)單的測(cè)試，或是推動(dòng)底盤觀察現(xiàn)象得出。
當(dāng)?shù)妆P沿著 X 軸平移時(shí)：
當(dāng)?shù)妆P沿著 Y 軸平移時(shí)：
當(dāng)?shù)妆P繞幾何中心自轉(zhuǎn)時(shí)：
將以上三個(gè)方程組相加，得到的恰好是根據(jù)「?jìng)鹘y(tǒng)」方法計(jì)算出的結(jié)果。這種計(jì)算方式不僅適用于O-長(zhǎng)方形的麥輪底盤，也適用于任何一種全向移動(dòng)的機(jī)器人底盤。
Makeblock 麥輪底盤的組裝
理論分析完成，可以開(kāi)始嘗試將其付諸實(shí)踐了。
第一步，組裝矩形框架。
第二步，組裝電機(jī)模塊。
由于麥輪底盤的四個(gè)輪子速度有約束關(guān)系，必須精確地控制每個(gè)輪子的速度，否則將會(huì)導(dǎo)致輥?zhàn)优c地面發(fā)生滑動(dòng)摩擦，不僅會(huì)讓底盤運(yùn)動(dòng)異常，還會(huì)讓麥輪的壽命減少。所以必須使用編碼電機(jī)。
第三步，將電機(jī)模塊安裝到框架上。
第四步，將麥輪安裝到框架上。
第五步，安裝電路板并接線。
編碼電機(jī)必須配上相應(yīng)的驅(qū)動(dòng)板才能正常工作。這里使用的 Makeblock 編碼電機(jī)驅(qū)動(dòng)板，每一塊板可以驅(qū)動(dòng)兩個(gè)電機(jī)。接線順序在下文中會(huì)提及，也可以隨意接上，在代碼中定義好對(duì)應(yīng)的順序即可。
第六步，裝上電池。
至此，一個(gè)能獨(dú)立運(yùn)行的麥輪底盤就完成了。
控制程序
根據(jù)麥輪的底盤的運(yùn)動(dòng)學(xué)模型，要完全控制它的運(yùn)動(dòng)，需要有三個(gè)控制量：X軸速度、Y軸速度、自轉(zhuǎn)角速度。要產(chǎn)生這三個(gè)控制量，有很多種方法，本文將使用一個(gè) USB 游戲手柄，左邊的搖桿產(chǎn)生平移速度，右邊的搖桿產(chǎn)生角速度。
首先將一個(gè) USB Host 模塊連接到 Orion 主板的 3 口。
然后插上一個(gè)無(wú)線 USB 游戲手柄。
然后再添加其他細(xì)節(jié)，就大功告成啦！
麥克納姆輪的有點(diǎn)和缺點(diǎn)都是非常明確的！采用麥克納姆輪 的車子大都移動(dòng)異常靈活，戰(zhàn)術(shù)機(jī)動(dòng)性能非常好；但是這種輪胎的越野性能卻非常差，跨越障礙的能力甚至不如普通輪胎，特別是當(dāng)坡度較大的時(shí)候，甚至還會(huì)溜 坡。所以配備這種車胎的設(shè)備大多是一些場(chǎng)地競(jìng)技機(jī)器人和室內(nèi)倉(cāng)儲(chǔ)機(jī)器人等，而前面所說(shuō)的那臺(tái)叉車也只能在路況較好的鋪裝路面跑跑。 | 
QQ好友和群
QQ空間
騰訊微博
騰訊朋友
收藏
淘帖
頂
踩
