信號與系統(tǒng)之周期信號的傅立葉級數(shù)表示：
信號表示為正交函數(shù)集
連續(xù)信號傅立葉級數(shù)性質
離散信號的傅里葉級數(shù)
連續(xù)信號的傅里葉級數(shù)
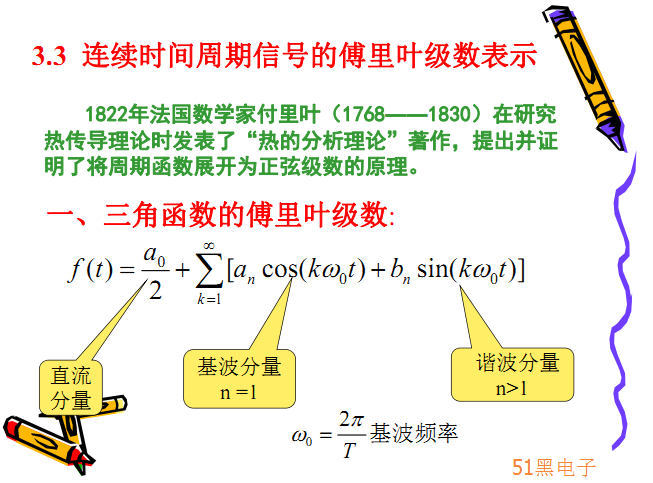
周期信號的傅立葉級數(shù)表示
本章要點
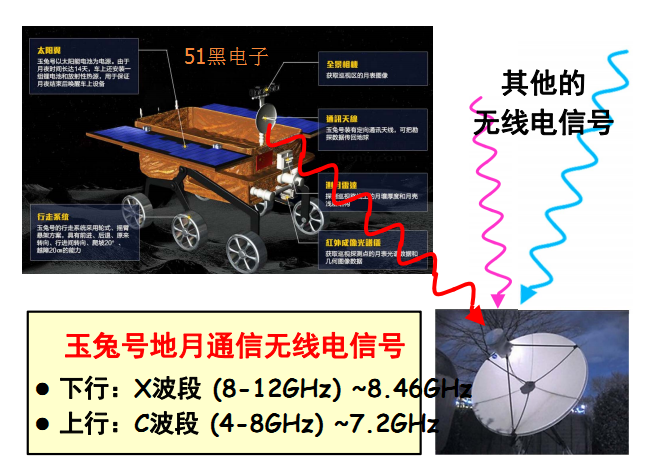
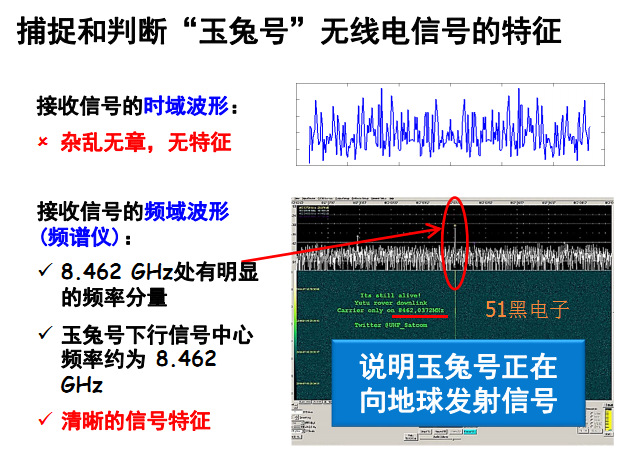
輸入信號的波形如果是矩形，
輸出的波形發(fā)生畸變，
畸變的規(guī)律不明顯。
輸入信號的波形是余弦，
輸出的波形仍是同頻率余弦，
只是振幅和相位發(fā)生變化。
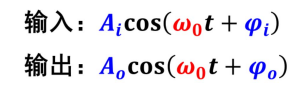
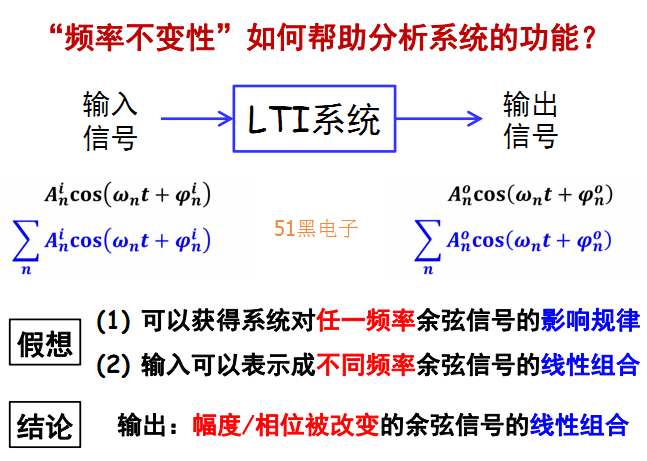
傅里葉的兩個主要觀點
(1) 周期信號可表示為呈諧波關系余弦信號的加權和
(2) 非周期信號可表示為連續(xù)頻率余弦信號的加權積分
第三章圍繞第一個觀點，闡述分解方法和物理含義：
數(shù)學形式：傅里葉級數(shù)
物理含義：頻譜（用另外的坐標系刻畫信號特征）
變換域分析——就是選取完備的正交函數(shù)集來最佳逼近信號，或者說，信號用完備的正交函數(shù)集來展開，其展開系數(shù)就是信號的變換表示。不同的變換域的區(qū)別就在于選取不同的正交完備集。
變換域分析的目的：主要是簡化分析。付里葉變換主要從信號分量的組成情況去考察信號的頻率特性。從而便于研究信號的傳輸和處理問題。
信號表示為正交函數(shù)集
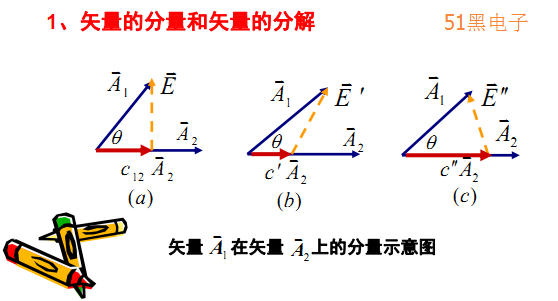
信號表示為正交函數(shù)分量的原理與矢量分解為正交矢量的概念類似。
完整的pdf格式課件文檔51黑下載地址（共36頁）：
信號6.pdf
(1.01 MB, 下載次數(shù): 32)
2018-11-1 22:58 上傳
點擊文件名下載附件
信號
|
