|
自動控制原理課程設計-基于雙閉環PID控制的一階倒立擺控制系統設計
倒立擺是一個非線性、不穩定系統,經常作為研究比較不同控制方法的典型例子。設計一個倒立擺的控制系統,使倒立擺這樣一個不穩定的被控對象通過引入適當的控制策略使之成為一個能夠滿足各種性能指標的穩定系統。 倒立擺的設計要求是使擺桿盡快地達到一個平衡位置,并且使之沒有大的振蕩和過大的角度和速度。當擺桿到達期望的位置后,系統能克服隨機擾動而保持穩定的位置。實驗參數自己選定,但要合理符合實際情況,控制方式為雙PID控制,并利用 MATLAB進行仿真,并用simulink對相應的模塊進行仿真。 倒立擺控制系統的工作原理是:由軸角編碼器測得小車的位置和擺桿相對垂直方向的角度,作為系統的兩個輸出量被反饋至控制計算機。計算機根據一定的控制算法,計算出空置量,并轉化為相應的電壓信號提供給驅動電路,以驅動直流力矩電機的運動,從而通過牽引機構帶動小車的移動來控制擺桿和保持平衡。 首先畫出一階倒立擺控制系統的原理方框圖 一階倒立擺控制系統示意圖如圖所示: 分析工作原理,可以得出一階倒立擺系統原理方框圖: 一階倒立擺控制系統動態結構圖 下面的工作是根據結構框圖,分析和解決各個環節的傳遞函數!
1.一階倒立擺建模 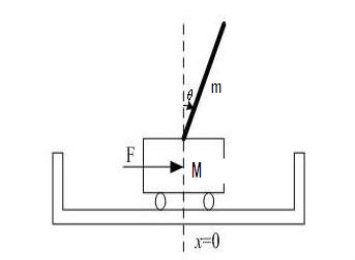 在忽略了空氣流動阻力,以及各種摩擦之后,可將倒立擺系統抽象成小車和勻質桿組成的系統,如下圖所示,其中: 在忽略了空氣流動阻力,以及各種摩擦之后,可將倒立擺系統抽象成小車和勻質桿組成的系統,如下圖所示,其中:
M:小車質量 m:為擺桿質量 J:為擺桿慣量 F:加在小車上的力 x:小車位置 θ:擺桿與垂直向上方向的夾角 l :擺桿轉動軸心到桿質心的長度 根據牛頓運動定律以及剛體運動規律,可知: 
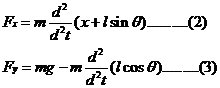
得 (3)小車水平方向上的運動為 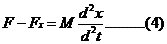
聯列上述4個方程,可以得出 一階倒立精確氣模型: 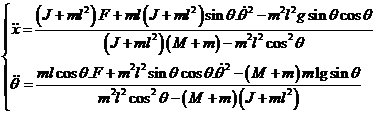
式中J為擺桿的轉動慣量: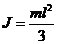 若只考慮θ在其工作點附近θ0=0附近(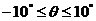 )的細微變化,則可以近似認為: )的細微變化,則可以近似認為:  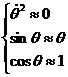 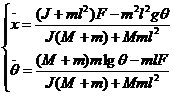
若取小車質量M=2kg,擺桿質量m=1kg,擺桿長度2l =1m,重力加速度取g= ,則可以得 ,則可以得 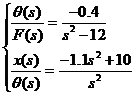 一階倒立擺簡化模型: 一階倒立擺簡化模型:
  拉氏變換 拉氏變換
即 G1(s)= 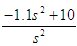 ; G2(s)= ; G2(s)= 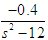 一階倒立擺環節問題解決! 2.電動機驅動器 選用日本松下電工MSMA021型小慣量交流伺服電動機,其有關參數如下: 驅動電壓:U=0~100V 額定功率:PN=200W 額定轉速:n=3000r/min 轉動慣量:J=3×10-6kg.m2 額定轉矩:TN=0.64Nm 最大轉矩:TM=1.91Nm 電磁時間常數:Tl=0.001s 電機時間常數:TM=0.003s 經傳動機構變速后輸出的拖動力為:F=0~16N;與其配套的驅動器為:MSDA021A1A,控制電壓:UDA=0~±10V。 若忽略電動機的空載轉矩和系統摩擦,就可以認為驅動器和機械傳動裝置均為純比例環節,并假設這兩個環節的增益分別為Kd和Km。 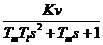
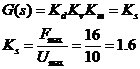 即D3(s)=1.6 電動機驅動器部分問題解決!
3.雙閉環PID控制器設計 剩下的問題就是如何確定控制器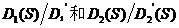 的結構和參數。 的結構和參數。 (一)內環控制器的設計 
其中,Ks=1.6為伺服電動機與減速機構的等效模型 1.控制器的選擇 內環系統未校正時的傳遞函數為 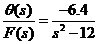 對于內環反饋控制器D2(s)可有PD,PI,PID三種可能的結構形式,怎么選取呢?這里,不妨采用繪制各種控制器結構下“系統根軌跡”的辦法加以分析比較,從之選出一種比較適合的控制器結構。 各種控制器的開環傳函的傳遞函數分別為: 在MATLAB下輸入以下程序用“湊試”的方法畫根軌跡圖: num=[分子]; den=[分母]; xlabel('Real Axis'); ylabel('Imag Axis'); axis([橫、縱坐標范圍]); title('Root Locus'); grid; rlocus(num,den) 下圖為各種控制器下的系統根軌跡。 (a) PD (b) PD
(c)PI d) PID 從根軌跡不難發現,采用PD結構的反饋控制器,結構簡單且可保證閉環系統的穩定。所以,選定反饋控制器的結構為PD形式的控制器。 2.控制器參數的選定 首先暫定K=-20。這樣可以求出內環的傳遞函數為: 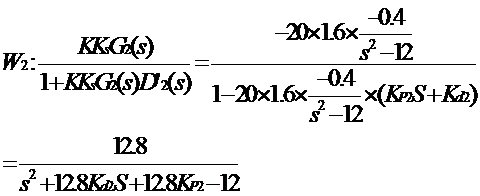

注釋:工程上常用阻尼比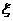 =0.707作為二階系統最優解! =0.707作為二階系統最優解! 3.系統內環的simulink仿真及結果 
仿真結果為: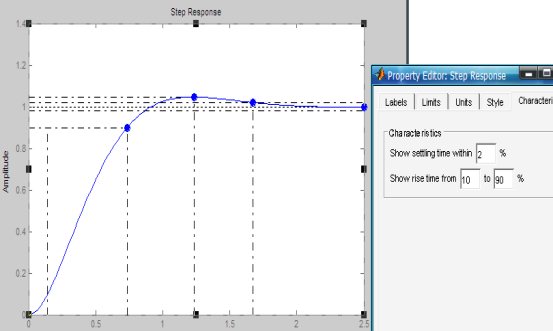
(二)外環控制器的設計 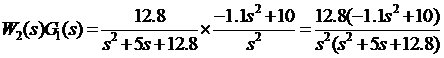
可見,系統開環傳遞函數可視為一個高階(4階)且帶有不穩定零點的“非最小相位系統”,為了便于設計,需要首先對系統進行一些簡化處理(否則,不便利用經典控制理論與方法對它進行設計)。 1.系統外環模型的降階 (1)對內環等效閉環傳遞函數的近似處理 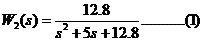
將高次項 忽略,有 忽略,有 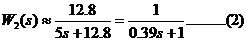
近似條件可由頻率特性導出,即 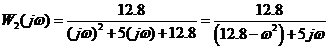
由(2)得: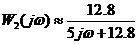 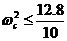 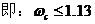
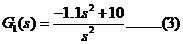
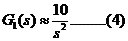
由(3)得: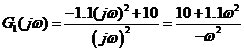 由(4)得: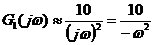 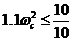 ,所以,有 ,所以,有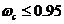 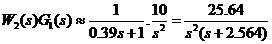
近似條件為: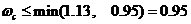 2.控制器設計 設加入的調節器為 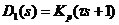 ,同時,為使系統有較好的跟隨性能,采用單位反饋 ,同時,為使系統有較好的跟隨性能,采用單位反饋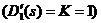 來構成外環反饋通道,如圖所示: 來構成外環反饋通道,如圖所示: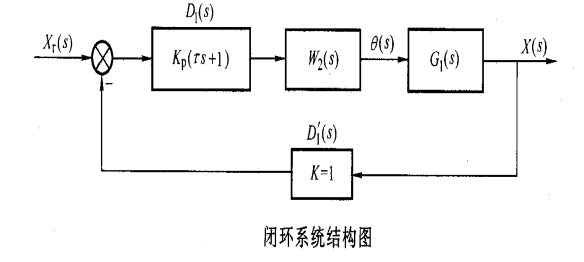 
取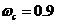  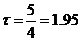 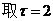 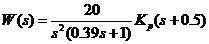
再由“典型Ⅱ型”系統Bode圖特性( 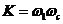 )知: )知: 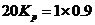 
3.用simulink對小車的位置在階躍信號輸入下的響應進行仿真: 系統框圖為 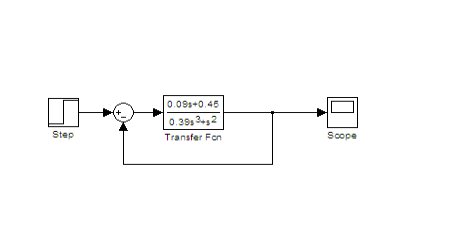
仿真結果: 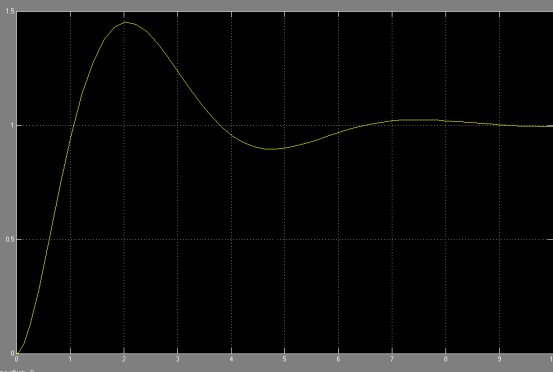
倒立擺位置在階躍信號下的響應
3.系統的simulink仿真 連接圖如下: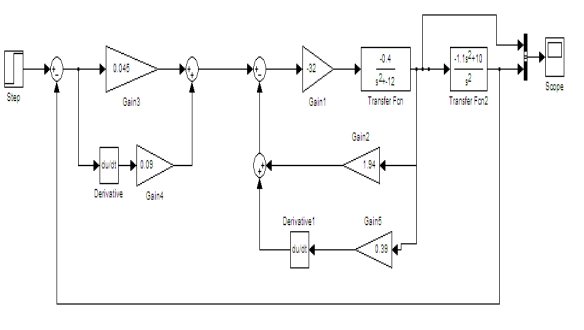 仿真結果為: 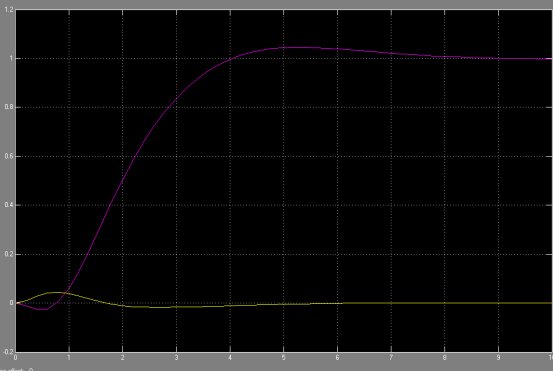
倒立擺在階躍信號下擺桿和小車位置的響應 從圖中可以看出建立的一階倒立擺控制系統在matlab中能夠實現倒立擺的要求,能通過電動機牽引機構帶動小車的移動來控制擺桿和保持平衡。 為了進一步驗證在不同擺桿下的,該一階倒立擺控制系統是否還具有魯棒特性,分別取擺桿不同的質量和擺長,進行simulink仿真!
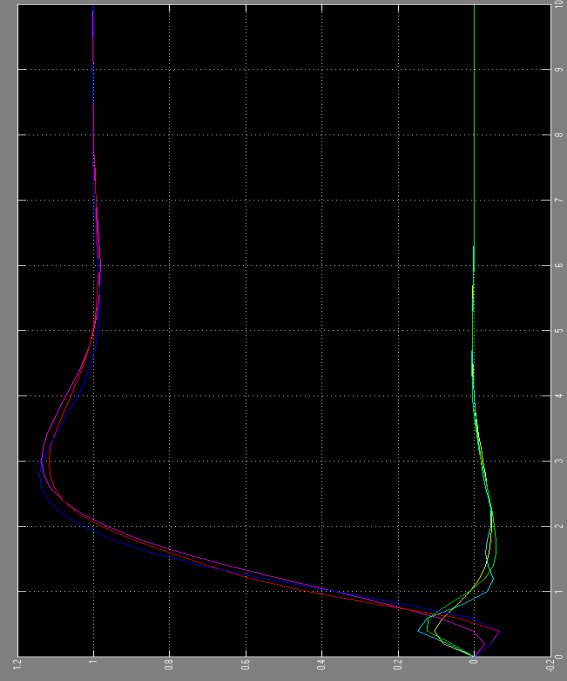
由圖可知,建立的一階倒立擺模型在不同擺長下能實現要求。但擺長不能過長!同理,建立的一階倒立擺模型在不同質量的擺桿下能也實現要求,但同樣不能過重! 五、課程設計心得 1、通過實驗了解了一階倒立擺是的非線性、不確定性、不穩定系統和約束限制,同時倒立擺也是經常作為研究比較不同控制方法的典型例子。 2、對一階倒立擺控制系統的研究使我了解到倒立擺還有二階倒立擺、三階倒立擺,甚至四階倒立擺,同時還涉及到起擺的問題!增加了了倒立擺研究的興趣! 3、建立的一階倒立擺控制系統忽略了許多因素,應用一些簡化處理,即建立的只是一階倒立擺控制系統的簡化模型。當擺桿的質量和擺長超過一定范圍,系統失效,所以該系統有待改進!
完整的Word格式文檔51黑下載地址:
 一級倒立擺控制系統設計.doc
(511 KB, 下載次數: 60)
一級倒立擺控制系統設計.doc
(511 KB, 下載次數: 60)
2018-10-23 15:40 上傳
點擊文件名下載附件
下載積分: 黑幣 -5
|