這是我上個月做的過程控制的設計，
用了幾個禮拜，
simulink的模型和結果太大發不上來
課題是
實驗一 過程控制系統建模
實驗二 PID 控制
實驗三 串級控制
實驗四 解耦控制系統
實驗五 比值控制
實驗一過程控制系統建模 常見的工業過程動態特性的類型有哪幾種？通常的模型都有哪些？在Simulink 中建立相應模型，并求單位階躍響應曲線。 1 單容過程模型 1）無自衡單容過程的階躍響應實例 2） 自衡單容過程的階躍響應實例 2 多容過程模型 3） 有相互影響的多容過程的階躍響應實例 4） 無相互影響的多容過程的階躍響應實例 某二階系統的模型為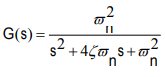 二階系統的性能主要取決于?，?兩個參數。試利用Simulink 仿真兩個參數的變化對二階系統輸出響應的影響，加深對二階系統的理解，分別進行下列仿真： （1）?? 2 不變時，?分別為0.1, 0.8, 1.0, 2.0 時的單位階躍響應曲線； （2）?? 0.8 不變時，?分別為2, 5, 8, 10 時的單位階躍響應曲線。 實驗二 PID 控制 利用Simulink 仿真軟件進行如下實驗： 1. 建立如圖所示的實驗Simulink 原理圖。 2. 雙擊原理圖中的PID 模塊，出現參數設定對話框，將PID控制器的積分增益和微分增益改為0，使其具有比例調節功能，對系統進行純比例控制。 3. 進行仿真，觀測系統的響應曲線，分析系統性能；然后調整比例增益，觀察響應曲線的變化，分析系統性能的變化。 P=1 P=5 P=10 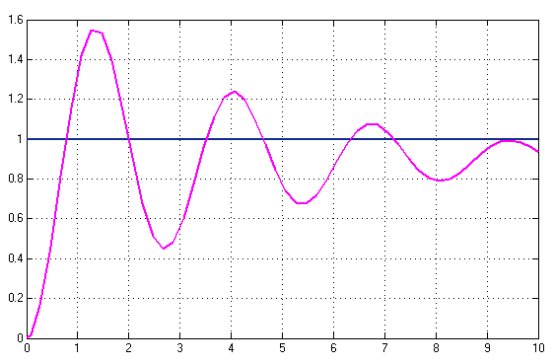 由以上三組響應曲線可以看出，純比例控制對系統性能的影響為：比例調節的余差隨著比例帶的加大而加大，減小比例帶就等于加大調節系統的開環增益，其后果是導致系統真激烈震蕩甚至不穩定，比例帶很大時，被調量可以沒有超調，但余差很大，調節時間也很長，減小比例帶就引起被調量的來回波動，但系統仍可能是穩定的，余差相應減少。 4. 重復（步驟2,3），將控制器的功能改為比例微分控制，觀測系統的響應曲線，分析比例微分的作用。 P=2;d=1 P=5;d=2 P=2;d=2 P=5;d=2 由以上四組響應曲線可以看出，比例微分控制對系統性能的影響為：可以提高系統的穩定性，引入適當的微分動作可以減小余差，并且減小了短期最大偏大，提高了振蕩頻率 5. 重復（步驟2,3），將控制器的功能改為比例積分控制，觀測系統的響應曲線，分析比例積分的作用。 P=2;i=1 P=5;i=1 P=2;i=2 P=5;i=2 由以上響應曲線可以看出，比例積分控制對系統性能的影響為：消除了系統余差，但降低了穩定性，PI調節在比例帶不變的情況下，減小積分時間TI（增大積分增益I），將使控制系統穩定性降低、振蕩加劇、調節過程加快、振蕩頻率升高 6. 重復（步驟2,3），將控制器的功能改為比例積分微分控制，觀測系統的響應曲線，分析比例積分微分的作用。 P=2;i=1;d=1 P=5;i=1;d=1 P=2;i=2;d=1 P=5;i=2;d=1 P=2;i=1;d=2 P=5;i=1;d=2 由以上幾組響應曲線可以看出，比例積分微分控制對系統性能的影響為：提高系統穩定性，抑制動態偏差，減小余差，提高響應速度，當微分時間較小時, 提高微分時間可以減小余差，提高響應速度并減小振蕩，當微分時間較大時，提高微分時間，振蕩會加劇。 7. 將PID 控制器的積分微分增益改為0，對系統進行純比例控制。不斷修改比例增益，使系統輸出的過度過程曲線的衰減比n=4，記下此時的比例增益值。 經過調整，當比例P=1時，終值r=0.5，第一個波峰值y1=0.72，第二個波峰值y2=0.55，衰減比約為4，如下圖所示 8. 修改比例增益，使系統輸出的過度過程曲線的衰減比n=2，記下此時的比例增益值。 經過調整，當比例P=12時，終值r=0.93，第一個波峰值y1=1.6，第二個波峰值y2=1.25，衰減比約為2，如下圖所示 9. 修改比例增益，使系統輸出呈現臨界振蕩波形，記下此時的比例增益。 P=100 P=1000 由圖可知，kp值越大，系統衰減比越小。故要使系統呈現臨界波形，可使kp趨于無窮大 10. 將PID 控制器的比例、積分增益進行修改，對系統進行比例積分控制。不斷修改比例、積分增益，使系統輸出的過渡過程曲線的衰減比n=2,4,10，記下此時比例和積分增益。
n=2 經過調整，當比例P=2，I=0.6時 終值r=1，第一個波峰值y1=1.30，第二個波峰值y2=1.16，衰減比約為2，如下圖所示 n=4 經過調整，當比例P=2.9，I=0.42時 終值r=1，第一個波峰值y1=1.28，第二個波峰值y2=1.07，衰減比約為4 n=10 經過調整，當比例P=1.23，I=0.02時 終值r=0.62，第一個波峰值y1=0.82，第二個波峰值y2=0.64，衰減比約10 11. 將PID 控制器的比例、積分、微分增益進行修改，對系統進行比例積分控制。不斷修改比例、積分、微分增益，使系統輸出的過度過程曲線的衰減比n=2,4,10，記下此時比例、積分、微分增益。
n=2 經過調整，當比例P=6，I=1，D=0.05時 終值r=1，第一個波峰值y1=1.5，第二個波峰值y2=1.25，衰減比約為2 n=4 經過調整，當比例P=6，I=0.5，D=0.05時 終值r=0.97，第一個波峰值y1=1.36，第二個波峰值y2=1.06，衰減比約為4 n=10 經過調整，當比例P=11，I=0.05，D=2時 終值r=0.92，第一個波峰值y1=1.3，第二個波峰值y2=0.96，衰減比約為10 實驗三 串級控制 串級控制系統仿真。已知某串級控制系統的主副對象的傳遞函數 Go1，Go2 分別為： 副回路干擾通道的傳遞函數為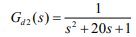： （1） 畫出串級控制系統的方框圖及相同控制對象下的單回路控制系統方框圖。 （2） 用 Simulink 畫出上述兩個系統的仿真框圖 串級控制系統的方框圖如下所示： 單回路控制系統方框圖如下所示： （3） 選用 PID 控制器，整定主副控制器的參數，使該串級控制系統性能良好，并繪制相應的單位階躍響應曲線。 經過不斷試驗，當PID Controller為主控制器輸入比例系數為360，積分系數為30，微分系數為60時；當PID Controller1為副控制器輸入比例系數為5，積分系數為0，微分系數為0時；系統階躍響應達到比較滿意的效果，系統階躍響應如下圖所示： 采用這套PID參數時 一次擾動作用下的階躍響應： 二次擾動下的階躍響應： （4） 比較單回路控制系統及串級控制系統在相同的副擾動下的單位階躍響應曲線，并說明原因 單回路控制系統在相同的副擾動下的單位階躍響應曲線： 一次擾動作用下的階躍響應： 二次擾動下的階躍響應： 比較上圖故可知串級系統由于副回路的存在對擾動的抑制能力更強。因擾動經干擾通道進入回路后首先影響副回路的輸出，副回路反饋后引起副控制器立即動作，力圖消弱干擾影響，使得干擾經過副回路的抑制后再進入主回路，對主回路的輸出影響大為減弱 實驗四 解耦控制系統 在例題中若輸入輸出之間傳遞關系改為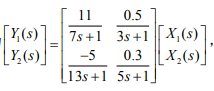 其他參數不變，試利用對角陣解耦方法實現系統的過程控制。 (1) 求系統相對增益以及系統耦合分析 由題得系統靜態放大系數矩陣為[k11,k12;k21,k22]=[11,0.5;-5,0.3] 即系統的第一放大系數矩陣為：p=[p11,p12;p21,p22]=[k11,k12;k21,k22]= [11,0.5;-5,0.3] 系統的相對增益矩陣為：Λ=[0.57,0.43;0.43,0.57] 由相對增益矩陣可以得知，控制系統輸入、輸出的配對選擇是正確的；通道間存在較強的相互耦合，應對系統進行解耦分析。 系統的輸入、輸出結構如下圖所示 （2）確定解耦調節器 根據解耦數學公式求解對角矩陣，即 [N11(s),N12(s);N21(s),N22(s)]=1/{Gp11(s)Gp22(s)-Gp12(s)Gp21(s)}*[Gp22(s),-Gp12(s);-Gp21(s),Gp11(s)]=1/(216.2s^2+82.5s+5.8)*[128.7s^2+52.8s+3.3, -13.65s^2-3s-0.15; 825s^2+440s+55, 128.7s^2+52.8s+3.3] 采用對角矩陣解耦后，系統的結構如下圖所示： 解耦前后系統的simulink階躍仿真框圖及結果如下： 1.不存在耦合時的仿真框圖及結果 2.系統耦合simulink仿真框圖及結果 3.對角矩陣解耦后的仿真框圖和結果 對比圖1和圖2可知，本系統的耦合影響主要體現在幅值變化和響應速度上，但影響不顯著。其實不進行解耦通過閉環控制仍有可能獲得要求品質。 對比圖1和圖3可知，采用對角解耦器后系統的響應和不存在耦合結果一樣，采用對角實現了系統解耦。解耦后系統可按兩個獨立的系統進行分析和控制。 (3).控制器形式選擇與參數整定 通過解耦，原系統已可看成兩個獨立的單輸入輸出系統。考慮到PID應用的廣泛性和系統無靜差要求，控制器形式采用PI形式。 PI參數整定通過解耦的兩個單輸入輸出系統進行，整定采取試誤法進行。 當x1y1通道Kp=20，Ki=3時系統的階躍響應如圖： 當x2y2通道Kp=35，Ki=5時系統階躍響應如圖： (4）系統仿真 采用對角矩陣解耦時，控制系統如下圖所示： 為了比較解耦和不解耦兩種情況，分別列出兩種情況的Simulink框圖和仿真結果。 解耦時系統的Simulink仿真框圖及結果（第二幅圖中的響應曲線從上往下依次是通道x2y2的輸入波形和響應波形、通道x1y1的輸入波形和響應波形以及隨機擾動波形）： 不解耦時系統的Simulink仿真框圖及結果（第二幅圖中的響應曲線在t=1s處從上往下依次是通道x2y2的輸入波形和響應波形、通道x1y1的輸入波形和響應波形以及隨機擾動波形）： 由圖對比結果可知，系統解耦后系統的動態響應有一定改善，但改善不大，這是由于耦合較弱所致。因此當要求不高時，系統可以不采取解耦措施。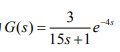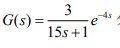 實驗五 比值控制 在例一中如系統傳遞函數為 其他參數不變，試對其進行單閉環比值控制系統仿真分析，并討論 分母中“15”變化?10% 時控制系統的魯棒性。 （1）分析從動量無調節器的開環系統穩定性。 由控制理論知，開環穩定性分析是系統校正的前提。系統穩定性的分析可利用Bode圖進行，編制MATLAB Bode圖繪制程序（M-dile）如下： clear all close all T=15;K0=3;tao=4; num=[K0];den=[T,1]; G=tf(num,den,'inputdelay',tao); margin(G) 執行該程序得系統的Bode圖如圖所示，可見系統是穩定的。幅值裕量為6.77dB，對應增益為2.2 (2)選擇從動量控制器形式及整定其參數。 根據工程整定的論述，選擇PI形式的控制器，即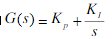 。 本處采用穩定邊界法整定系統。先讓IK=0，調整pK使系統等幅振蕩（由穩定性分析圖知在pK=2.2附近時系統震蕩），即使系統處于臨界穩定狀態。 系統Simulink框圖如下所示 調節Kp=0.3,Kf=0.02時，系統響應圖如下所示，基本達到了振蕩臨界要求 （3）系統過程仿真。 單閉環比值控制過程相當于從動量變化的隨動控制過程。假定主動量由一常值10加幅度為0.3的隨機擾動構成，從動量受均值為0、方差為1的隨機干擾。主動量和從動量的比值根據工藝要求及測量儀表假定為3。 系統的控制過程Simulink仿真框圖如圖所示。其中控制常量及隨機擾動采用封裝形式。 主動控制量的封裝結構如下： 運行結果如下所示（圖中曲線從上往下分別為從動量跟蹤結果、主動量給定值和隨機干擾）： 可見除初始時間延時外，從動量較好地跟隨主動量變化而變化，并且基本維持比值3，有效地克服了主動量和從動量的擾動。 （4）單閉環比值控制系統魯棒性分析 要求分母中“15”變化10%，即積分時間為13.5~16.5，分析系統魯棒性。 系統仿真框圖如下圖所示 延時選擇模塊Subsystem的展開圖如下所示 改變積分時間常數為13.5，13.8——16.5共11個值。經過運行后在工作空間繪圖（使用語句：plot（tout，simout）；hold on；grid on）即可見到下圖的仿真結果。 從仿真結果可見，隨著延時環節的變化，從動量跟隨主動量的規律有較小變化，但并未改變系統穩定性及精度，說明系統在積分時間發生10%?變化時仍能正常工作，系統的魯棒性較強。
以上圖文的Word格式文檔下載(內容和本網頁上的一模一樣,方便大家保存):
過控實驗.docx
(956.59 KB, 下載次數: 81)
2018-7-9 21:35 上傳
點擊文件名下載附件
下載積分: 黑幣 -5
| 
QQ好友和群
QQ空間
騰訊微博
騰訊朋友
收藏
淘帖
頂
踩
