久久久久久久999_99精品久久精品一区二区爱城_成人欧美一区二区三区在线播放_国产精品日本一区二区不卡视频_国产午夜视频_欧美精品在线观看免费

 找回密碼
 立即注冊

QQ登錄

只需一步，快速開始

搜索
查看: 4067|回復: 0
打印 上一主題 下一主題
收起左側

啟發式搜索,簡單遺傳算法,候選消除算法源碼 人工智能實驗報告

[復制鏈接]
跳轉到指定樓層
樓主
ID:365689 發表于 2018-7-5 16:13 | 只看該作者 回帖獎勵 |倒序瀏覽 |閱讀模式
本科實驗報告
課程名稱：   人工智能        
實驗項目：1.啟發式搜索2.基于產生式系統的問
題求解3簡單遺傳算法4候選消除算法
實驗地點：實驗樓110
專業班級：物聯網1501 學號：2015001962
學生姓名：程*
指導教師：強*   

實驗一 啟發式搜索
一 實驗目的
熟悉和掌握啟發式搜索的定義、估價函數和算法過程，并利用A算法求解相關問題，理解求解流程和搜索順序。
先熟悉啟發式搜索算法；
     用C、C++、JAVA或python             語言編程實現實驗內容。
二 實驗內容以及原理
估價函數
在對問題的狀態空間進行搜索時，為提高搜索效率需要和被解問題的解有關的大量控制性知識作為搜索的輔助性策略。這些控制信息反映在估價函數中。
估價函數的任務就是估計待搜索節點的重要程度，給這些節點排定次序。估價函數可以是任意一種函數，如有的定義它是節點x處于最佳路徑的概率上，或是x節點和目標節點之間的距離等等。在此，我們把估價函數f(n)定義為從初始節點經過n節點到達目標節點的最小代價路徑的代價估計值，它的一般形式是：
     f(n) = g(n) + h(n)
其中g(n)是從初始節點到節點n的實際代價，g(n)可以根據生成的搜索樹實際計算出來；h(n)是從n到目標節點的最佳路徑的代價估計，h(n)主要體現了搜索的啟發信息。
啟發式搜索過程的特性
（1）可采納性
當一個搜索算法在最短路徑存在的時候能保證能找到它，我們就稱該算法是可采納的。所有A*算法都是可采納的。
（2）單調性
一個啟發函數h是單調的，如果

    對所有的狀態ni和nj，其中nj是ni的子孫，h(ni)- h(nj)≤cost(ni,nj),其中cost(ni,nj)是從ni到nj實際代價。
    目標狀態的啟發函數值為0，即h(Goal)=0.

具有單調性的啟發式搜索算法在對狀態進行擴展時能保證所有被擴展的狀態的f值是單調遞增（不減）。
（3）信息性
比較兩個啟發策略h1和h2，如果對搜索空間中的任何一個狀態n都有h1(n)≤h2(n)，就說h2比h1具有更多的信息性。
一般而言，若搜索策略h2比h1有更多的信息性，則h2比h1考察的狀態要少。但必須注意的是更多信息性需要更多的計算時間，從而有可能抵消減少搜索空間所帶來的益處。

3.常用的啟發式搜索算法
（1）局部擇優搜索算法（瞎子爬山法）
瞎子爬山法是最簡單的啟發式算法之一。該算法在搜索過程中擴展當前節點并估價它的子節點。最優的子節點別選擇并進一步擴展；該子節點的兄弟節點和父節點都不再被保留。當搜索到達一種狀態，該狀態比它的所有子狀態都要好，則搜索停止。因此，該算法的估價函數可表示為f(n) = h(n)。
在一個限定的環境下，瞎子爬山法可能會極大的提高搜索的效率，但是對整個搜索空間而言，可能得不到全局最優解。
（2）最好優先搜索法（有序搜索法）
該算法的估價函數采用f(n) = g(n) + h(n)，在搜索過程中算法使用OPEN表和CLOSE表來記錄節點信息：OPEN表中保留所有已生成而未考察的節點；CLOSE表中保留所有已訪問過的節點。算法在每一次搜索過程中都會對OPEN表中的節點按照每個節點的f值進行排序，選擇f值最小節點進行擴展。算法的描述如下：
①把起始節點S放到OPEN表中，計算f(S),并把其值與節點S聯系起來。
②若OPEN是個空表，則算法失敗退出，無解。
③從OPEN表中選擇一個f值最小的節點i。結果有幾個節點合格，當其中有一個為目標節點時，則選擇此目標節點，否則就選擇其中任一個節點作為節點i。
④把節點i從OPEN表中移出，并把它放入到CLOSED的擴展節點表中。
⑤若節點i是個目標節點，則成功退出，求得一個解。
⑥擴展i，生成其全部后繼節點。對i的每個后繼節點j：

    計算f(j)。
    如果j既不在OPEN表中，也不在CLOSED表中，則用估價函數f將其添加到OPEN表。從j加一指向其父輩節點i的指針，以便一旦找到目標節點時記住一個解答路徑。
    如果j已則OPEN表中或CLOSED表中，則比較剛剛對j計算過的f值和前面計算過的該節點在表中的f的值。若新的f值較小，則
        以此值取代舊值。
        從j指向i，而不是指向它的父輩節點。
        若節點j在CLOSED表中，則把它移回OPEN表。

⑦轉向②。
三 實驗儀器
macOS操作系統
四 實驗步驟/設計實現
設計估價函數
設計算法步驟
編寫實驗程序
2
8
3
1
6
4
7

5
  • 用啟發式搜索方法求解九宮問題。
1
2
3
8

4
7
6
5

五 實驗代碼
六 實驗結果以及分析
實驗二 基于產生式系統的問題求解
一 實驗目的
熟悉和掌握產生式系統的構成和運行機制，掌握基于規則推理的基本方法和技術。
1.先熟悉產生式系統的基本概念；
    2.用C、C++或JAVA             語言編程實現實驗內容。

二 實驗內容以及原理
產生式系統（Production system）首先由波斯特（Post）于1943年提出的產生式規則（Production rule）而得名，他們用這種規則對符號串進行置換運算，后來，美國的紐厄爾和西蒙利用這個原理建立了一個人類的認知模型（1965年），同年，斯坦福大學利用產生式系統結構設計出第一個專家系統DENDRAL。
產生式系統用來描述若干個不同的以一個基本概念為基礎的系統。這個基本概念就是產生式規則或產生式條件和操作對象的概念。
在產生式系統中，論域的知識分為兩部份：
  • 事實：用于表示靜態知識，如事物、事件和它們之間的關系；
（2）規則：用于表示推理過程和行為


一個產生式系統由三個部分組成，如圖所示：
  • 總數據庫：用來存放與求解問題有關的數據以及推理過程環境的當前狀態的描述。
產生式規則庫：主要存放問題求解中的規則。（3）控制策略：其作用是說明下一步應該選用什么規則，也就是說如何應用規則。




通常從選擇規則到執行操作分三步：
  • 匹配：把當前數據庫和規則的條件部分相匹配。如果兩者完全匹配，則把這條規則稱為觸發規則。
（2）沖突解決：當有一個以上的規則條件部分和當前數據庫相匹配時，就需要解決首先使用哪一條規則——沖突解決。
1）專一性排序：如果某一規則的條件部分比另一條規則的條件部分所規定的情況更為專門，則這條規則有較高的優先權。
2）規則排序：如果規則編排順序就表示了啟用的優先級，則稱之為排序。
3）數據排序：把規則條件部分的所有條件按優先級次序編排起來，運行時首先使用在條件部分包含較高優先級數據的規則。4）規模排序：按規則的條件部分的規模排列優先級，優先使用被滿足的條件較多的規則。
5）就近排序：把最近使用的規則放在最優先的位置。
6）上下文限制：把產生式規則按他們所描述的上下文分組，也就是說按上下文對規則分組，在某種上下文條件下，只能從與其相對應的那組規則中選擇可應用的規則。
7）使用次數排序：把使用頻率較高的排在前面。


（3）操作：執行規則的操作部分，經過修改以后，當前數據庫將被修改。
問題描述：用基于產生式系統的方法求解傳教士和野人問題
有N個傳教士和N個野人來到河邊準備渡河，河岸有一條船，每次至多可供K個乘渡，問傳教士為了安全起見，應如何規劃擺渡方案，使得任何時刻，河岸兩邊以及船上的野人數目總是不超過傳教土的數目，即求解傳教士和野人從左岸全部擺渡到右岸的過程中，任何時刻滿足M（傳教士數）≥C（野人數）和M+C≤K的擺渡方案。

三 實驗儀器
macos
四 實驗步驟/設計實現
設計估價函數
設計算法步驟
編寫實驗程序
五 實驗代碼

六 實驗結果以及分析
實驗三 遺傳算法
一 實驗目的
熟悉和掌握遺傳算法的基本思想和基本方法，通過實驗培養學生利用遺傳算法進行問題求解的基本技能，并且了解進化計算其他分支的基本思想和基本方法。


先熟悉進化計算中遺傳算法的基本思想和流程；
   用C、C++、JAVA或Prolog             語言編程實現實驗內容。

二 實驗內容以及原理
生物群體的生存過程普遍遵循達爾文的物競天擇、適者生存的進化準則。群體中的個體根據對環境的適應能力而被大自然所選擇或淘汰。進化計算(evolutionary computation, EC)就是通過模擬自然物群進化的一類非常魯棒的優化算法，它們模擬群體(其中組成群體的每個個體表示搜索問題解空間中的一個解)的集體學習過程，從任意初始群體出發，通過隨機選擇、變異和交叉過程，使群體進化學習到搜索空間中越來越好的區域。進化計算中選擇過程使群體中適應性好的個體比適應性差的個體有更多的機會遺傳到下一代中，交叉算子將父代信息結合在一起并他們遺傳給下一代個體，而變異過程在群體中引入新的變種。進化計算包括遺傳算法(evolutionary algorithm,EA)、進化策略(evolution strategy, ES)、進化編程(evolutionary programming, EP)、遺傳編程(genetic programming, GP)。
遺傳算法是模仿生物遺傳學和自然選擇機理，通過人工方式構造的一類優化搜索算法，是對生物進化過程的一種數學仿真，是進化計算的一種最重要形式。遺傳算法為那些那些難以找到傳統數學模型的難題找出了一個解決方法。自從Holland于1975年在其著作《Adaptation in Natural and Artificial Systems》中首次提出遺傳算法
以來，經過近30年的研究，現在已發展到一個比較成熟的階段，并且在實際中已經得到了很好的應用。
1.簡單遺傳算法的構成要素
（1）染色體編碼和解碼方法
在實現對一個問題用遺傳算法之前，我們必須先對問題的解空間進行編碼，以便使得它能夠由遺傳算法進行操作。解碼就是把遺傳算法操作的個體轉換成原來問題結構的過程。常見的編碼方法有：二進制編碼、浮點數編碼、格雷碼等。以二進制為例：假設某一參數的取值范圍是[A，B]，A＜B，我們有長度為l的二進制編碼串來表示該參數，將[A，B]等分成2l-1個子部分，每個等分的長度為δ，則它能夠產生2l種不同的編碼。
         00000000000…0000000000 = 0  →A
         00000000000…0000000001 = 1     →A + δ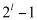
         11111111111……1111111111 =→B
二進制編碼的最大缺點是使得遺傳算法操作的個體位串太長，這容易降低遺傳算法的運行效率，很多問題采用其他編碼方法可能更有利。如對于函數優化問題，浮點數編碼方法就更有效，而二進制編碼方法不但容易降低遺傳算法的運行效率，而且會產生精度損失。浮點數編碼方法是指個體的每個染色體用某一范圍內的一個浮點數表示，個體的編碼長度就等于問題變量的個數。
在實際運用遺傳算法解決問題時，一般都需要根據具體的問題采用合適的編碼方法，這樣更有利于遺傳算法搜索到問題的最優解。
（2）適應度函數
遺傳算法在進化搜索中基本上不用外部信息，僅用目標函數也就是適應度函數為依據。適應度函數是用于度量問題中每一個染色體優劣程度的函數，體現了染色體的適應能力。遺傳算法的目標函數不受連續可微的約束且定義域可以是任意集合。但對適應度函數有一個要求就是針對輸入可以計算出的能加以比較的結果必須是非負的。
在具體應用中，適應度函數的設計要結合求解問題本身的要求而設計。因為適應度函數對個體的評估是遺傳算法進行個體選擇的唯一依據，因此適應度函數的設計直接影響到遺傳算法的性能。對于很多問題，可以直接把求解問題的目標函數作為適應度函數使用，但也存在很多問題需要進行一定的轉換才能使得目標函數可以用作遺傳算法的適應度函數。
（3）遺傳算子
遺傳算法主要有三種操作算子：選擇(selection)、交叉(crossover)、變異(mutation)。
○1選擇算子
選擇算子根據個體的適應度函數值所度量的優劣程度選擇下一代個體。一般地，選擇算子將使適應度函數值較大的個體有較大的機會被遺傳到下一代，而適應度函數值較小的個體被遺傳到下一代的機會較小。一般常采用的選擇算子是賭輪選擇機制。賭輪選擇算子的基本原理如下。
令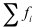表示種群的適應度值之總和，表示群體中第i個染色體的適應度值，則第i個個體產生后代的能力正好為其適應度值與群體適應度值的比值。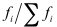
賭輪選擇算子在個體數不太多時，有可能出現不正確反映個體適應度的選擇過程，也就是說適應度高的個體有可能反而被淘汰了。為了改進賭輪選擇算子的這種缺點，有很多改進的交叉選擇算子。如：最佳個體保存法、期望值方法、排序選擇方法、聯賽選擇方法、排擠方法等。
○2交叉算子
在自然界生物進化過程中，起核心作用的是生物遺傳基因的重組(加上變異)。同樣，遺傳算法中，起核心作用的是遺傳操作的交叉算子。所謂交叉算子就是把兩個父代個體的部分結構加以替換重組而生成新個體的操作。通過交叉，遺傳算法的搜索能力得以飛躍提高。
交叉算子設計一般與所求解的具體問題有關，但都應該考慮以下兩點：○A設計的交叉算子必須能保證前一代中優秀個體的性狀能在后一代的新個體中盡可能得到遺傳和繼承。○B交叉算子與問題的編碼是相互聯系的，因此，交叉算子設計和編碼設計需協調操作，也就是所謂的編碼—交叉設計。
對于字符串編碼的遺傳算法，交叉算子主要有一點交叉、兩點交叉、多點交叉和一致交叉等。其中一點交叉的主要操作過程如下。假設兩個配對個體為P1、P2分別如下所示。經過一點交叉后，得到兩個新的個體P1’、P2’。

對于實數編碼的遺傳算法，交叉算子主要是采用算術交叉算子。假設兩個配對個體分別為P1＝(x1,y1)和P2=(x2,y2)。在P1和P2進行算術交叉后得到的兩個新個體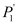和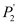分別可由下式計算得到。
      



○3變異算子
變異算子是改變數碼串中某個位置上的數碼。遺傳算法中引入變異算子有兩個目的：其一是使遺傳算法具有局部的隨機搜索能力。當遺傳算法通過交叉算子已接近最優解領域時，利用變異算子的這種局部隨機搜索能力可以加速遺傳算法向最優解收斂。一般在這種情況下，遺傳算法的變異概率應取較小的值，否則接近最優解的積木塊會因為變異而遭到破壞。其二是使遺傳算法可以維持較好的群體多樣性，以防止遺傳算法出現未成熟收斂現象。此時，遺傳算法的變異概率應取較大的值。
遺傳算法中，交叉算子具有很好的全局搜索能力，是算法的主要操作算子。變異算子具有較好的局部搜索能力，是算法的輔助操作算子。遺傳算法通過交叉和變異這一對相互配合又相互競爭的操作而使其具備兼顧全局和局部的均衡搜索能力。變異算子除了基本的變異算子外，還有很多有效的變異算子。如逆轉變異算子、自適應變異算子等。對于字符串編碼的遺傳算法，基本變異算子就是隨機的從個體中選擇某些基因位，然后以一定的概率對這些基因位進行翻轉變異，也就是把這些基因位中為0的基因位以概率Pm變為1，為1的基因為以概率Pm變為0。對于實數編碼的遺傳算法，一般采用隨機變異的方式，使變異個體的每一個變量分量加上一個隨機數，一般使用均勻分布的隨機數或者是高斯分布的隨機數。
（4）基本遺傳算法運行參數
N：群體大小，即群體中所含個體的數量，一般取20～100
T：遺傳算法的終止進化代數，一般取100～500
pc：雜交概率，一般取0.4～0.99
pm：變異概率，一般取0.0001～0.1
pr：復制概率


三 實驗儀器
macos
四 實驗步驟/設計實現
設計估價函數
設計算法步驟
編寫實驗程序
五 實驗代碼


六 實驗結果以及分析

實驗四 候選消除算法
一 實驗目的
熟悉和掌握示例學習的基本思想和基本方法，通過實驗培養學生利用示例學習進行問題求解的基本技能。
先熟悉示例學習中常見算法的基本思想和流程；
用C、C++、JAVA或Prolog             語言編程實現實驗內容。
利用所學的知識及實驗結果，來完成實驗報告的各項內容。


二 實驗內容以及原理
示例學習(Learning from examples)又稱為實例學習或從例子中學習，它是通過從環境中取得若干與某概念有關的例子，經歸納得出一般性概念的一種學習方法。在這種學習方法中，外部環境(教師)提供的是一組例子(正例和反例)，這些例子實際上是一組特殊的知識，每一個例子表達了僅適用于該例子的知識，示例學習就是要從這些特殊知識中歸納出適用于更大范圍的一般性知識，它將覆蓋所有的正例并排除所有反例。其任務是：給定函數f(未知)的實例集合，返回一個近似于f的函數h—h稱為假設，所有h的集合稱為假設空間。
Simon于1974年在一篇論文中，把從示例學習的問題描述為使用示教例子來指導對規則的搜索，并提出了兩空間模型。



其中，實例空間模型為所有示教例子的集合。規則空間模型為所有規則的集合。兩者的關系是：系統對實例空間的搜索完成實例選擇，并將這些選中的活躍實例提交解釋過程；解釋過程對實例經過適當的轉化，將這些實例變換為規則空間中的特定概念，以引導規則空間的搜索。
對實例空間而言示教例子的質量和實例空間的搜索是兩個值得注意的問題：
（1）高質量的例子是無二義性的，它可以為規則空間的搜索提供可靠的指導；另外示教例子的排列次序也會影響學習。
（2）搜索實例空間的目的在于選擇合適的例子，使得這些例子能證實或否定規則空間中假設的集合H。常見的搜索方法有：選擇對劃分規則空間最有利的實例；利用H中的假設過濾掉與那些期望為真的實例；選擇新實例等。
對規則空間而言推理方法和規則表示是兩個值得注意的問題：
（1）常見的歸納推理方法有：a.常量轉化成變量；b.取消部分條件；c.放松條件；d.形成閉合區域；e.沿概念樹上溯等。
（2）規則表示要注意：a.對規則的表示應適合歸納推理b.規則的表示與實例的表示一致；c.規則空間中應包含要求的規則。
常見的示例學習的算法有，尋找極大特殊假設法、候選消除算法、精練算子法、產生測試法等。這里我們主要介紹一下候選消除算法。
*候選消除算法
該方法以整個規則空間為初始的假設規則集合H。依據實例中的信息，系統對集合H進行一般化或特殊化處理，逐步縮小H。最后H收斂到只含有要求的規則。上述過程可稱為H的變型過程，該過程主要是利用了H中規則與規則之間的偏序關系來進行規則的搜索。其算法如下：
（1）初始化G和S，G包含最一般假設，S包含最特殊假設。
（2）接受一個新的實例x，若x是正例，則從G中刪除不包含x的概念，更新S，盡可能對S進行一般化以覆蓋x；若x是反例，則從S中刪除包含x的概念，更新G，盡可能對G進行特殊化使之不覆蓋x。
（3）重復2，直到G=S
（4）輸出G和S
如果G和S都為空，表示沒有找到學習的概念描述;如果G和S相等且不為空，表示找到了學習的概念描述，且算法停止。


三 實驗儀器
macOS
四 實驗步驟/設計實現
設計估價函數
設計算法步驟
編寫實驗程序
五 實驗代碼

六 實驗結果以及分析


部分源碼：
  1. #include <stdio.h>
  2. #include <conio.h>
  3. #include <stdlib.h>
  4. #include <time.h>
  5. #include <iostream>

  7. typedef struct Chrom                           // 結構體類型，為單個染色體的結構；
  8. {
  9.         short int bit[6];//一共6bit來對染色體進行編碼，其中1位為符號位。取值范圍-64~+64
  10.         int fit ;//適應值
  11.         double rfit;//相對的fit值，即所占的百分比
  12.         double cfit;//積累概率
  13. }chrom;                                       
  14. //定義將會用到的幾個函數；
  15. void *evpop (chrom popcurrent[4]);//進行種群的初始化
  16. int x (chrom popcurrent);
  17. int y (int x);
  18. void *pickchroms (chrom popcurrent[4]);//選擇操作
  19. void *pickchroms_new (chrom popcurrent[4]); // 基于概率分布
  20. void *crossover (chrom popnext[4]);//交叉操作
  21. void *mutation (chrom popnext[4]);//突變
  22. double r8_uniform_ab ( double a, double b, int &seed );//生成a~b之間均勻分布的數字
  23. chrom popcurrent [4];                        // 初始種群規模為；
  24. chrom popnext [4];                           // 更新后種群規模仍為；
  25. void main ()                                    // 主函數；
  26. {
  27.         int num ;                                    // 迭代次數；
  28.         int i ,j, l,Max ,k;
  29.         Max=0;                                      // 函數最大值

  31.         printf("\nWelcome to the Genetic Algorithm！\n");  //
  32.         printf("The Algorithm is based on the function y = -x^2 + 5 to find the maximum value of the function.\n");

  34. enter:printf ("\nPlease enter the no. of iterations\n請輸入您要設定的迭代數 : ");
  35.         scanf("%d" ,&num);                           // 輸入迭代次數，傳送給參數 num；

  37.         if(num <1)                                 
  38.                 goto enter ;                                 // 判斷輸入的迭代次數是否為負或零，是的話重新輸入；
  39.         //不同的隨機數可能結果不同？？那是當所設置的迭代次數過少時，染色體的基因型過早地陷入局部最優
  40.         srand(time(0));  
  41.         evpop(popcurrent );    // 隨機產生初始種群；
  42.         //是否需要指定x的取值范圍呢？6bit來表示數字，第一位為符號位，5bit表示數字大小。所以，取值范圍為-32~+31
  43.         Max = popcurrent[0].fit;//對Max值進行初始化

  45.         for(i =0;i< num;i ++)                          // 開始迭代；
  46.         {

  48.                 printf("\ni = %d\n" ,i);                 // 輸出當前迭代次數；

  50.                 for(j =0;j<4; j++)
  51.                 {
  52.                         popnext[j ]=popcurrent[ j];           // 更新種群；
  53.                 }

  55.                 pickchroms(popnext );                    // 挑選優秀個體；
  56.                 crossover(popnext );                     // 交叉得到新個體；
  57.                 mutation(popnext );                      // 變異得到新個體；

  59.                 for(j =0;j<4; j++)
  60.                 {
  61.                         popcurrent[j ]=popnext[ j];              // 種群更替；
  62.                 }

  64.         }  // 等待迭代終止；
  65. //對于真正隨機數是需要注意取較大的迭代次數
  66.         for(l =0;l<3; l++)
  67.         {
  68.                 if(popcurrent [l]. fit > Max )
  69.                 {
  70.                         Max=popcurrent [l]. fit;
  71.                         k=x(popcurrent [l]);//此時的value即為所求的x值
  72.                 }

  74.         }
  75.         printf("\n 當x等于 %d時，函數得到最大值為： %d ",k ,Max);
  76.         printf("\nPress any key to end ! " );

  78.         flushall();                                 // 清除所有緩沖區；
  79.         getche();                                   // 從控制臺取字符，不以回車為結束；

  81. }                                             



  85. void *evpop (chrom popcurrent[4])   // 函數：隨機生成初始種群；
  86. {
  87.         int i ,j, value1;
  88.         int random ;
  89.         double sum=0;
  90.         
  91.         for(j =0;j<4; j++)                            // 從種群中的第1個染色體到第4個染色體
  92.         {
  93.                 for(i =0;i<6; i++)                       // 從染色體的第1個基因位到第6個基因位
  94.                 {
  95.                         random=rand ();                     // 產生一個隨機值
  96.                         random=(random %2);                 // 隨機產生0或者1
  97.                         popcurrent[j ].bit[ i]=random ;       // 隨機產生染色體上每一個基因位的值，或；
  98.                 }  

  100.                 value1=x (popcurrent[ j]);                // 將二進制換算為十進制，得到一個整數值；
  101.                 popcurrent[j ].fit= y(value1); // 計算染色體的適應度值
  102.                 sum = sum + popcurrent[j ].fit;
  103.                 printf("\n popcurrent[%d]=%d%d%d%d%d%d  value=%d  fitness = %d",j, popcurrent[j ].bit[5], popcurrent[j ].bit[4], popcurrent[j ].bit[3], popcurrent[j ].bit[2], popcurrent[j ].bit[1], popcurrent[j ].bit[0], value1,popcurrent [j]. fit);
  104.                 // 輸出整條染色體的編碼情況，
  105.         }
  106.         //計算適應值得百分比，該參數是在用輪盤賭選擇法時需要用到的
  107.         for (j = 0; j < 4; j++)
  108.         {
  109.                 popcurrent[j].rfit = popcurrent[j].fit/sum;
  110.                 popcurrent[j].cfit = 0;//將其初始化為0
  111.         }
  112.         return(0);               
  113. }                                       


  116. int x (chrom popcurrent)  // 函數：將二進制換算為十進制；
  117. {//此處的染色體長度為，其中個表示符號位
  118.         
  119.         int z ;
  120.         z=(popcurrent .bit[0]*1)+( popcurrent.bit [1]*2)+(popcurrent. bit[2]*4)+(popcurrent .bit[3]*8)+( popcurrent.bit [4]*16);

  122.         if(popcurrent .bit[5]==1)  // 考慮到符號；
  123.         {
  124.                 z=z *(-1);                             
  125.         }

  127.         return(z );                           
  128. }                                    
  129. //需要能能夠從外部直接傳輸函數，加強魯棒性
  130. int y (int x)// 函數：求個體的適應度；
  131. {
  132.         int y ;
  133.         y=-(x *x)+5;                                // 目標函數：y= - ( x^ 2 ) +5；
  134.         return(y );            
  135. }
  136. //基于輪盤賭選擇方法，進行基因型的選擇
  137. void *pickchroms_new (chrom popnext[4])//計算概率
  138. {
  139.         int men;
  140.         int i;int j;
  141.         double p;
  142.         double sum=0.0;
  143.         //find the total fitness of the population
  144.         for (men = 0; men < 4; men++ )
  145.         {
  146.                 sum = sum + popnext[men].fit;
  147.         }
  148.         //calculate the relative fitness of each member
  149.         for (men = 0; men < 4; men++ )
  150.         {
  151.                 popnext[men].rfit = popnext[men].fit / sum;
  152.         }
  153.         //calculate the cumulative fitness,即計算積累概率
  154.         popcurrent[0].cfit = popcurrent[0].rfit;
  155.         for ( men = 1; men < 4; men++)
  156.         {
  157.                 popnext[men].cfit = popnext[men-1].cfit + popnext[men].rfit;
  158.         }
  159.         
  160.         for ( i = 0; i < 4; i++ )
  161.         {//產生0~1之間的隨機數
  162.                 //p = r8_uniform_ab ( 0, 1, seed );//通過函數生成0~1之間均勻分布的數字
  163.                 p =rand()%10;//
  164.                 p = p/10;
  165.                 if ( p < popnext[0].cfit )
  166.                 {
  167.                         popcurrent[i] = popnext[0];      
  168.                 }
  169.                 else
  170.                 {
  171.                         for ( j = 0; j < 4; j++ )
  172.                         {
  173.                                 if ( popnext[j].cfit <= p && p < popnext[j+1].cfit )
  174.                                 {
  175.                                         popcurrent[i] = popcurrent[j+1];
  176.                                 }
  177.                         }
  178.                 }
  179.         }
  180.         //  Overwrite the old population with the new one.
  181.         //
  182.         for ( i = 0; i < 4; i++ )
  183.         {
  184.                 popnext[i] = popcurrent[i];
  185.         }
  186.         return(0);
  187. }
  188. void *pickchroms (chrom popnext[4])          // 函數：選擇個體；
  189. {
  190.         int i ,j;
  191.         chrom temp ;                                // 中間變量
  192.         //因此此處設計的是個個體，所以參數是
  193.         for(i =0;i<3; i++)                           // 根據個體適應度來排序；（冒泡法）
  194.         {
  195.                 for(j =0;j<3-i; j++)
  196.                 {
  197.                         if(popnext [j+1]. fit>popnext [j]. fit)
  198.                         {
  199.                                 temp=popnext [j+1];
  200.                                 popnext[j +1]=popnext[ j];
  201.                                 popnext[j ]=temp;

  203.                         }  
  204.                 }               
  205.         }
  206.         for(i =0;i<4; i++)
  207.         {
  208.                 printf("\nSorting:popnext[%d] fitness=%d" ,i, popnext[i ].fit);
  209.                 printf("\n" );                     
  210.         }
  211.         flushall();/* 清除所有緩沖區 */                     
  212.         return(0);
  213. }   
  214. double r8_uniform_ab( double a, double b, int &seed )
  215. {
  216.         {
  217.                 int i4_huge = 2147483647;
  218.                 int k;
  219.                 double value;

  221.                 if ( seed == 0 )
  222.                 {
  223.                         std::cerr << "\n";
  224.                         std::cerr << "R8_UNIFORM_AB - Fatal error!\n";
  225.                         std::cerr << "  Input value of SEED = 0.\n";
  226.                         exit ( 1 );
  227.                 }

  229.                 k = seed / 127773;

  231.                 seed = 16807 * ( seed - k * 127773 ) - k * 2836;

  233.                 if ( seed < 0 )
  234.                 {
  235.                         seed = seed + i4_huge;
  236.                 }

  238.                 value = ( double ) ( seed ) * 4.656612875E-10;

  240.                 value = a + ( b - a ) * value;

  242.                 return value;
  243.         }
  244. }
  245. void *crossover (chrom popnext[4])              // 函數：交叉操作；
  246. {

  248.         int random ;
  249.         int i ;
  250.         //srand(time(0));
  251.         random=rand ();                             // 隨機產生交叉點；
  252.         random=((random %5)+1);                     // 交叉點控制在0到5之間；
  253.         for(i =0;i< random;i ++)                  
  254.         {
  255.                 popnext[2].bit [i]= popnext[0].bit [i];   // child 1 cross over
  256.                 popnext[3].bit [i]= popnext[1].bit [i];   // child 2 cross over
  257.         }

  259.         for(i =random; i<6;i ++)                      // crossing the bits beyond the cross point index
  260.         {
  261.                 popnext[2].bit [i]= popnext[1].bit [i];    // child 1 cross over
  262.                 popnext[3].bit [i]= popnext[0].bit [i];    // chlid 2 cross over
  263.         }  

  265.         for(i =0;i<4; i++)
  266.         {
  267.                 popnext[i ].fit= y(x (popnext[ i]));        // 為新個體計算適應度值；
  268.         }

  270.         for(i =0;i<4; i++)
  271.         {
  272.                 printf("\nCrossOver popnext[%d]=%d%d%d%d%d%d    value=%d    fitness = %d",i, popnext[i ].bit[5], popnext[i ].bit[4], popnext[i ].bit[3], popnext[i ].bit[2], popnext[i ].bit[1], popnext[i ].bit[0], x(popnext [i]), popnext[i ].fit);
  273.                 // 輸出新個體；
  274.         }
  275.         return(0);
  276. ……………………

  278. …………限于本文篇幅 余下代碼請從51黑下載附件…………
復制代碼

全部資料51hei下載地址（內含完整源碼）：
強彥.doc (712.88 KB, 下載次數: 14)



分享到:  QQ好友和群QQ好友和群 QQ空間QQ空間 騰訊微博騰訊微博 騰訊朋友騰訊朋友
收藏收藏1 分享淘帖 頂頂1 踩踩
回復

使用道具 舉報

您需要登錄后才可以回帖 登錄 | 立即注冊

本版積分規則

手機版|小黑屋|51黑電子論壇 |51黑電子論壇6群 QQ 管理員QQ:125739409;技術交流QQ群281945664

Powered by 單片機教程網

快速回復 返回頂部 返回列表
主站蜘蛛池模板： 国产精品久久久久久吹潮 | 在线观看毛片网站 | 亚洲91视频 | 亚洲精品视频在线播放 | 久久一本| 在线观看国产视频 | 中文字幕日韩在线 | 欧美三级在线 | 久久久久久久电影 | 亚洲欧美日韩高清 | 在线看无码的免费网站 | 亚洲午夜电影 | 亚洲第一区国产精品 | 91精品国产综合久久久久久 | 亚洲欧美精品国产一级在线 | 亚洲激情第一页 | 欧美久久一区二区三区 | 美女福利网站 | 羞羞网站在线观看 | 久久av.com| 亚洲二区视频 | 亚洲手机视频在线 | 国产精品视频网 | www.成人在线视频 | 国产日韩精品久久 | 国产成人高清 | 99久久婷婷国产综合精品 | 欧美a区 | 亚洲高清在线 | 夜夜爽99久久国产综合精品女不卡 | 看av电影 | 亚洲日本中文 | 久久久久国产一区二区三区 | 美女国产精品 | 中文字幕视频在线 | 一区二区三区中文字幕 | 日日艹夜夜艹 | 久久一二 | 二区av| 女同久久 | 日本久久精品视频 |