數學中有哪些看起來很不可思議的知識？

先來看個公式吧，這個盡管不難證明，但是還蠻有趣的~

一.平面幾何篇

1.（i）九點圓定理：三角形三邊的中點，三條高的垂足，垂心與各頂點連線的中點這九點共圓。（九點圓又稱歐拉圓、費爾巴哈圓）

（ii）費爾巴哈定理：三角形的九點圓與其內切圓以及三個旁切圓相切。

（iii）庫里奇-大上定理：九點圓的圓周上（任意取定）四點中任取三點做三角形，所有這四個三角形的九點圓圓心共圓。

2.西姆松（Simson）定理：過三角形外接圓上異于三角形頂點的任意一點作三邊或其延長線上的垂線，則三垂足共線。（此線常稱為西姆松線）

3.蝴蝶定理：設M為圓內弦PQ的中點，過M作弦AB和CD。設AD和BC各相交PQ于點X和Y，則M是XY的中點。（配個圖啦啦啦~）

4.君知物理學中有家喻戶曉的牛頓三大定律，殊不知平面幾何中也有牛頓三大定理（別鬧，當然是同一個牛頓），想當年剛知道時簡直膜拜~

牛頓定理1：完全四邊形三條對角線中點共線。

牛頓定理2：圓外切四邊形的兩條對角線的中點，及該圓的圓心，三點共線。推廣：和完全四邊形四邊相切的有心圓錐曲線的心的軌跡是一條直線,是完全四邊形三條對角線中點所共的線。

牛頓定理3：圓的外切四邊形的對角線的交點和以切點為頂點的四邊形對角線交點重合。（四線共點）

5.帕斯卡（Pascal）定理：圓錐曲線內接六邊形其三對邊的交點共線，與布列安桑定理對偶，是帕普斯定理的推廣。（至于后面兩個是什么，戳進去看就好了，當年也只是知道是什么并沒有用過~）

6.根心定理：三個兩兩不同心的圓，形成三條根軸，則要么三根軸兩兩平行，要么三根軸完全重合，否則三根軸兩兩相交，即此時三根軸必交于一點（三線共點），該點稱為三圓的根心。（根軸是對兩圓等冪的點集，是一條垂直于連心線的直線，特殊情形：若兩圓相交，則根軸就是連接二公共點的直線；若兩圓相切，則根軸就是過切點的公切線；）

7.五點共圓：（具體追根溯源請搜索密克（Miquel）定理）（不會證的孩紙還是先不要膜了，趕緊多讀書，不然還是naive~~）

2000年12月20日，參觀濠江中學時向該校師生出了一道求證“五點共圓”的平面幾何題：“假設：任意一個星形，五個三角形，外接圓交于五點。求證：這五點共圓。”

這道平面幾何題用規范的數學語言表述是這樣的：在任意五角星AJEIDHCGBF中，△AFJ、△JEI、△IDH、△HCG和△GBF各自的外接圓順次相交的交點分別為K、O、N、M、L。求證：K、O、N、M、L五點共圓。（確實很神奇~~）

8.雞爪定理（我也想知道有沒有好聽一點的名字啊親~）：設△ABC的內心為I，∠A內的旁心為J，AI的延長線交三角形外接圓于K，則KI=KJ=KB=KC。（注意紅線的形狀）

9.拿破侖（Napoléon）定理（據說是行軍打仗時證明的，也是厲害）：向任何三角形三邊分別向外側作等邊三角形，然后把這三個正三角形的中心連結起來所構成的三角形一定是等邊三角形。

這一定理可以等價描述為：若以任意三角形的各邊為底邊向形外作底角為60°的等腰三角形，則它們的中心構成一個等邊三角形。

一些引申：

1）四邊形上，類似的定理為凡·奧貝爾定理。

2）拿破侖定理本身為佩特諾-伊曼-道格拉斯定理的特例。

3）內拿破侖三角形的面積大于等于 0 給出外森比克不等式。

10.莫利（Morley）定理：將三角形的三個內角三等分，靠近某邊的兩條三分角線相交得到一個交點，則這樣的三個交點可以構成一個正三角形。這個三角形常被稱作莫利正三角形。

（題外話：聽高中同學說，某老師在外邊上課給純良的男孩紙們講：跟喜歡的女孩紙說隨便畫一個三角形，如果它的角三分線交點恰好是正三角形，就證明對她的愛是真心的。我向那個高中同學當即表示，這就是紅果果的欺騙啊~現在終于明白為什么自己還在汪汪汪了~~~）

11.歐拉線定理：任意三角形的外心、重心、垂心、九點圓圓心，依次位于同一直線上。（這條直線就叫三角形的歐拉線，且外心到重心的距離等于垂心到重心距離的一半）

12.沢山定理：圓P與圓O的內接四邊形ABCD的對角線AC、BD切于E、F，同時與圓O相切，則E、F與△ABD、△ACD的內心I、I'共線（四點共線）。

二.初等代數篇

1.歐拉公式：（出于對歐拉大神的無比景仰崇拜以及對這個公式特有的贊賞，答主一定要把它先放出來，不過對大家來講也許太熟悉了~）

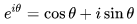，由此有一個經常被稱作所謂“上帝公式”的恒等式（得名源于將五個基本常數匯聚一堂）：  

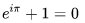
2.（i）對于任意的自然數n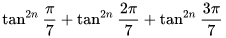， 的值都是一個正整數。

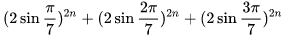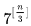（ii）對于任意的自然數n， 能被 整除。

三.組合數學篇

1.對于簡單多面體。設V為頂點數，E為棱數，F是面數，則 。

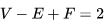對任意的平面圖，歐拉公式可以推廣為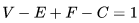： ，其中C為圖中連通分支數。

對非平面圖，歐拉公式可以推廣為：如果一個圖可以被嵌入一個流形M，則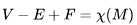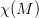： ， 是此流形的歐拉示性數，在流形的連續變形下是不變量。單連通流形（例如球面或平面）的歐拉特征值是2。

2.正多面體只有五種：正四面體、正六面體（正方體）、正八面體、正十二面體和正二十面體。

四、數學分析篇

1. 調和級數是發散的，然而：

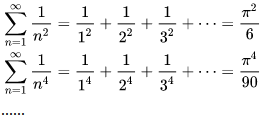
其實這些都是所謂的Riemann zeta function的特例，這個函數定義如下：

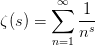
回到這部分開始給出的兩個等式，用Zeta函數的形式就分別為

事實上，我們還有  

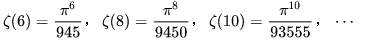
嗯，聰明的你一定會想到，肯定有個統一的公式！！好的，獎勵你一顆糖，哦不，一個公式：

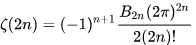
式中的 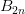是偶數項的Bernoulli數（每一項都是有理數，n>1的奇數n項均為0，其余請自行學習Bernoulli number），總的來講結果很美麗。如果你還知道生成函數概念的話，下面的結論希望你喜歡：

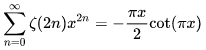
被驚艷到了有木有！！可是對于奇數的s,就沒有這樣漂亮的結果了，舉個還算能看的例子：

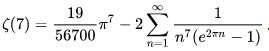
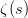這個函數實在是包羅萬象，十分迷人，許多很好的性質和漂亮的結論（上面的結果就是），甚至對于s=-1時，還有以下這個著名的等式：

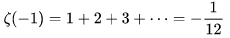
特別說明，s=-1時的情況是解析延拓意義下的，上面這個式子的等號的含義也和我們通常熟知的情形不同，然而大部分人看過的所謂的加加減減的證明更是民科之至，當作個好玩的東西就可以了，那種證明是錯誤的，為了不偏題太遠，不展開說了。它的一般結果為：

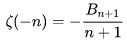
由Bernoulli數的性質就有

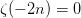
還有更多奇妙的性質，大家自行去wiki吧，哈哈~（復變函數簡直打開了新世界的大門~~）

五、數論篇

1. Fermat大定理推廣形式的恒等式：（以勾股定理為[2,2]型，Fermat大定理為[2,n]型為例）

(1). [3,3]型：

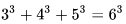
(2). [4,4]型：

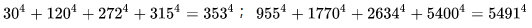
(3). [4,5]型：

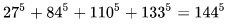
(4). [5,5]型：

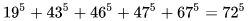
(5). [7,7]型：

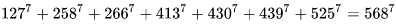
(6). [8,8]型：

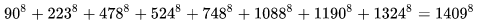
(7). [3,4]型：（無窮多個，太大就不寫在下面了，反正也不夠漂亮了）

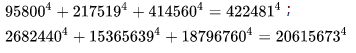
2. 整冪次和的其他恒等式：

(1). Euler四平方和恒等式及Lagrange的四平方和定理：前者的表述為“如果兩個數都能表示為四個平方數的和，則這兩個數的積也能表示為四個平方數的和。”后者則為“每一個正整數都可以表示為四個平方數之和。”

(2).Brahmagupta-Fibonacci定理：

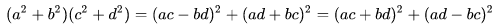
例如：

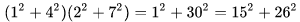
(3).
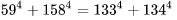