無線傳感器網絡是由大量的具有信息感知功能的傳感節點通過無線通信方式形成一個多跳的自組織網絡系統[1]。位置是判斷人或物體所處情形和環境的直接依據[2]，在無線傳感器網絡中利用節點發送與接收無線信號確定物體的位置稱為無線傳感器網絡節點定位[3]。根據定位機制，可將現有的定位算法分為兩類[4]：基于測距(Range-based)的定位算法和無需測距(Range-free)的定位算法[5]。Range-based的定位對網絡的硬件設施提出了較高的要求，各種測量技術也存在各自的局限性[6]。此外，Range-based的定位經常采用多次測量, 循環求精[7],這些都將產生大量計算和通信開銷[8]，因而基于測距定位算法并不適用于低功耗、低成本的應用領域[9]。與Range-based機制相比，Range-free定位機制對硬件的要求較低，因此，成本和功耗較低，且網絡生存能力強[10]，定位精度基本滿足實際需要，是目前研究工作的重點之一[11]。文中將柵格掃描定位算法得到的位置坐標作為初始位置估計，在此基礎上提出了一種改進的Range-free定位算法，減小了平均相對定位誤差。

Grid-Scan算法是在APIT算法中提出的一種典型的無需測距的定位算法[12]，文獻[13]提出的VGrid-Scan算法主要通過改變錨節點的通信半徑，但不影響未知節點搜索鄰居錨節點，從而縮小未知節點的定位區域，該方法在一定程度上提高了定位精度。

Grid-Scan算法分為3個步驟[15]：

第一步：網絡部署，待定位的未知節點搜索其通信范圍內所有錨節點，并記錄被搜索到的錨節點的ID和坐標信息，這些被搜索到的錨節點稱為鄰居錨節點。

第二步：將未知節點Uj所有鄰居錨節點的通信圓交集以其外接矩形代替，得到外接估計矩形ER (Estimative Rectangle)[14]。如圖1所示，ER的四條邊分別平行于x軸和y軸。ER的大小由式(1)確定。

圖1   外接估計矩形示意圖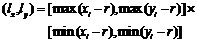

(lx，ly)為未知節點所屬的ER大小，i為錨節點下標，(xi，yi)為錨節點的位置坐標，r為錨節點的通信半徑。

第三步：劃分柵格并計算未知節點的坐標。設柵格的邊長為l，ER的長為 L×l，寬為 W×l，則ER可表示為L×W個柵格的集合G。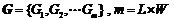

將網絡中所有柵格的初始值賦為0，Cm為柵格的中心，若ER內柵格Gm和Cm均位于n個鄰居錨節點的通信范圍內，則將柵格Gm賦值為n。ER內賦值最大的所有柵格組成的區域對應為一個未知節點的估計區域Ej，如圖2所示賦值最大的柵格組成的區域即為估計區域Ej，最后，計算該估計區域Ej的質心位置，實現對未知節點的定位。

圖2   ER內柵格賦值

文中通過對Grid-Scan定位算法的研究發現，該算法允許未知節點只存在一個鄰居錨節點的情況下進行定位，且在隨機產生的網絡拓撲中，未知節點的實際位置可能位于以估計位置到鄰居錨節點的距離為半徑的圓內，這樣的未知節點存在著可再定位性，對這些有可再定位性的未知節點，文中利用Grid-Scan算法允許一個錨節點定位的特點，采用最近錨節點對具有可再定位性的未知節點進行二次定位，提高定位精度。

首先由鄰居錨節點的位置信息可以得到未知節點的初始位置估計，然后利用鄰居錨節點坐標信息與初始位置估計的坐標信息得到未知節點更小更精確的位置估計區域，最后進行二次求精。改進算法具體分為3個階段。

(1)初始位置估計

設未知節點的鄰居錨節點個數為n，利用傳統的Grid-Scan算法對某未知節點進行定位，得到未知節點的初始位置估計坐標(xe，ye)，此時對應該未知節點ER區域內的柵格已被賦值完成，得到Ej區域所有被賦值為n的柵格Grid。

(2)判斷可再定位性

求出所有鄰居錨節點到該未知節點的信號強度，設未知節點接收到所有鄰居錨節點的信號強度為RSS，而RSS中的最大信號強度RSSu對應的錨節點即為最近錨節點。由式(3)計算初始位置估計到最近錨節點的距離dist。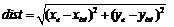

(xe，ye)為初始位置估計坐標，(xist，yist)為最近錨節點坐標，將dist代入 (4)可得初始位置到最近錨節點的理論信號強度RSSe。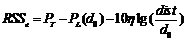

其中，PT為發送信號功率；PL(d0)為參考距離d0的路徑損耗功率；η為路徑損耗指數。當RSSu>RSSe時，判定未知節點存在可再定位性；當RSSu≤RSSe時，判定未知節點不可再定位，該未知節點最終定位的位置即為初始位置估計。

(3)柵格二次賦值

對可再定位的未知節點進行二次柵格掃描。計算Ej區域內所有柵格的Cm到最近錨節點的距離D。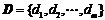

當dm>dist時，dm對應在Grid內的值不變；當dm < dist時，dm對應在Grid內的柵格值為n+1，賦值為n+1的柵格集合為Gridmap；由Gridmap產生一個新的估計區域ENj，計算ENj的質心位置得到最終定位的位置。

如圖2所示，設未知節點有三個鄰居錨節點A1，A2，A3相交區域為Ej，A1為最近錨節點，在Ej區域內得到未知節點的初始位置估計，得到Ej區域內柵格賦值為3的Grid，以初始位置到A1的距離dist為半徑對Ej區域進行柵格掃描得到估計區域ENj，ENj區域內柵格值在Grid基礎上加1，得到ENj區域所有被賦值為4的柵格集合Gridmap，計算最終定位坐標。

圖3   二次柵格掃描示意圖

文中實驗在Matlab平臺上進行，設節點個為N，并在100×100m監測區域內產生隨機的拓撲場景，節點通信半徑為r，柵格邊長為l，節點發送信號功率PT=0dB，參考距離d0=1m，參考距離d0的路徑損耗功率PL(d0)=55dB，路徑損耗指數η=4。將文中改進算法記為SGrid-Scan算法，并與傳統的Grid-Scan算法及文獻[13]中的VGrid-Scan算法在歸一化的平均相對定位誤差上進行對比。其中，VGrid-Scan算法依然采用文獻[13]中錨節點通信半徑的設定方法，設置為節點通信半徑的0.7倍。

網絡中每個可定位節點的誤差為：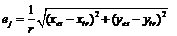

其中：(xes，yes) 為未知節點最終的估計坐標，(xtr，ytr)為未知節點的實際坐標，r為節點的通信半徑。網絡中所有未知節點的歸一化的平均相對定位誤差為: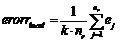

其中：文中實驗設k=100，即產生100個隨機網絡拓撲，nr為可定位的節點個數。

為了使兩種算法的仿真誤差更具對比性，將每次產生的隨機網絡拓撲場景分別提供給SGrid-Scan算法、Grid-Scan算法和VGrid-Scan算法進行仿真，確保三種算法在相同環境下進行定位誤差的計算，增加實驗數據對比的可靠性。

通過式(1)可以發現，節點的通信半徑可以影響未知節點的外接矩形的大小，進而影響鄰居錨節點個數。設節點個數N=200，錨節點個數為40，柵格邊長l=2m。

圖4   通信半徑對算法定位誤差的影響               如圖6所示，柵格邊長越小，三種算法的定位誤差越低，且SGrid-Scan算法的定位誤差較Grid-Scan算法平均減小了2.37%；SGrid-Scan算法較VGrid-Scan算法的定位精度平均提高了1.15%；隨著柵格邊長的增大，三種算法的定位誤差就越接近，但SGrid-Scan算法的定位誤差始終最低。

錨節點密度影響鄰居錨節點個數，鄰居錨節點個數可以影響估計區域Ej的大小。在固定區域內。設節點個數N=200，節點通信半徑r=20m，柵格邊長l=2m。

圖5   錨節點個數對算法定位誤差的影響

如圖5所示，三種算法的定位誤差均隨錨節點個數增加而逐步減小。SGrid-Scan算法的定位誤差較Grid-Scan算法平均減小了3.92%；SGrid-Scan算法較VGrid-Scan算法的定位精度平均提高了1.77%。

節點總數是衡量網絡密集度的一個重要參數，因此仿真了節點總數對兩種算法定位性能的影響。設節點通信半徑r=20m，錨節點個數為0.2N，柵格邊長l=2m。

圖6   節點個數對算法定位誤差的影響

如圖6所示，隨著節點個數的增多，網絡密集度隨之變大，三種算法的定位誤差均隨之減小。SGrid-Scan算法較傳統Grid-Scan算法的定位誤差平均減小了4.11%。當節點個數N=150時，兩種算法定位精度的差值最大，為5.12%；SGrid-Scan算法較VGrid-Scan算法的定位精度平均提高了1.45%。

由Grid-Scan算法的定位原理可知，柵格的邊長會對估計區域Ej邊緣的柵格數量產生影響，從而影響Ej質心的位置。設節點個數N=200，錨節點個數為40，節點的通信半徑r=20m。

圖7   柵格邊長對算法定位誤差的影響

如圖6所示，柵格邊長越小，三種算法的定位誤差越低，且SGrid-Scan算法的定位誤差較Grid-Scan算法平均減小了2.37%；SGrid-Scan算法較VGrid-Scan算法的定位精度平均提高了1.15%；隨著柵格邊長的增大，三種算法的定位誤差就越接近，但SGrid-Scan算法的定位誤差始終最低。

結束語文中首先采用傳統的Grid-Scan算法得到一個初始位置估計，然后通過對初始位置估計到最近錨節點位置的理論信號強度與未知節點到最近錨節點的信號強度進行對比，判斷未知節點的可再定位性，再以最近錨節點到初始位置的距離為半徑對可再定位的未知節點進行二次柵格掃描，從而進一步縮小了未知節點的定位區域，一定程度上提高了定位精度。仿真結果表明，在變通信半徑、變錨節點個數、變節點個數和變柵格邊長的條件下，改進算法均有效降低了平均相對定位誤差。

完整的Word格式文檔51黑下載地址：
二次柵格掃描的無線傳感器網絡定位算法.docx (265.47 KB, 下載次數: 6)

2018-6-4 15:12 上傳

點擊文件名下載附件
定位算法.pdf