|
轉速閉環直流調速系統的構建與動態數學模型的建立 摘要:本文論述了直流電動機調速系統的調速方法,并分析開環,閉環調速系統系統的各個組成部分,以及系統的機械特性。逐步推導出各個環節的傳遞函數以及數學模型,根據各個環節的關系最后得到系統的傳遞函數以及動態模型,并簡單分析系統的穩定條件。 關鍵詞:直流電動機,調速系統,數學模型,靜特性, 動態特性, 穩定性
0.引言一般直流電動機具有相同的工作原理和應用特性,按類型主要分為直流有刷電動機和直流無刷電動機,后期由于采用了永磁磁場,使直流無刷電動機擺脫一般直流電動機的傳統設計和結構,伴隨著高性能永磁材料、微電子技術、自動控制技術和電力電子技術的進步,永磁無刷直流電機得到了迅速發展[1]。由于克服了機械換向裝置的固有缺點,無刷直流電機具有壽命長、調速性能優越,體積小、重量輕、效率高、轉動慣量小、電磁兼容性好等諸多優點。無刷直流電機的應用和研究受到了廣泛的重視,憑其技術優勢在許多場合取代了其它種類的電動機[1]。特別是在微特電機領域,在小功率、高轉速的調速領域,無刷直流電機占據著主要位置。由直流電機的轉速公式: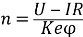 (0.1) (0.1) U:電樞定壓 φ:主磁通 R:電樞電阻 可知,直流電機調速方案有三種: (1) 調節電樞供電電壓U (2) 改變電動機主磁通φ (3) 改變電樞回路電阻R
1.轉速閉環直流調速系統的構建1.1 V-M系統的組成及其機械特性晶閘管整流器-電動機調速系統的原理圖如圖1.1所示,圖中VT是晶閘管整流器通過調節觸發裝置GT的控制電壓UC來移動觸發脈沖的相位,改變可控整流器平均輸出電流電壓Ud,從而實現直流電動機的平滑調速。 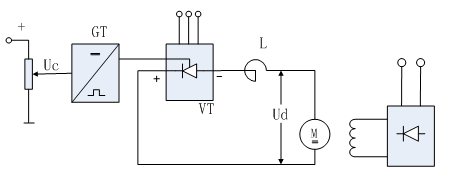
圖1.1 V-M系統原理圖 當電流波形連續時,V-M系統的機械特性方程式為 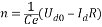 (1.1) (1.1)
式中 Ce—電動機在額定磁通下的電動勢系數,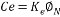 其中,由于電壓波形存在脈動,造成了電流波形的脈動,脈動的電流波形使V-M系統主電路可能出現電流連續和斷續兩種情況。具體原因不在此祥述。 圖1.2繪出了完整的V-M系統機械特性,其中包含了整流狀態和逆變狀態,電流連續區和電流斷續區。由圖可見,當電流連續時,特性還比較硬;斷續段特性則很軟,而且呈顯著的非線性的上翹,使電動機的理想空載轉速很高;連續區和斷續區的分界線對應于Ø=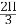 的曲線。只要電流連續,晶閘管可控整流器就可以看成一個線性的可控電壓源。 的曲線。只要電流連續,晶閘管可控整流器就可以看成一個線性的可控電壓源。 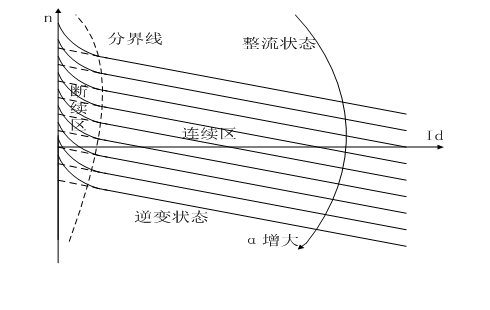
圖1.2 V-M系統機械特性 1.2 V-M系統的穩態性能指標 任何一臺需要控制轉速的設備,其生產工藝對調速性能都有一定的要求。對于調速系統轉速控制的要求有以下三個方面: - 調速 :在一定的最高轉速和最低轉速范圍內,有級或無級地調節轉速;
- 穩速:以一定的精度在所需轉速穩定運行,在各種干擾下不允許有過大的轉速波動,以確保產品質量;
- 加,減速:頻繁地起動,制動的設備要求加速,減速盡量快,以提高生產率;不宜受劇烈速度變化的機械則要求起動,制動盡量平穩。
為了進行定量的分析,針對前兩項要求誕生出兩個調速指標,稱為調速范圍和靜差率。這兩個指標便稱作調速系統的穩態性能指標。 生產機械要求電動機提供的最高轉速nmax與最低轉速nmin之比便是調速范圍,用D表示,即 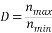 (1.2) (1.2)
當系統在某一轉速下運行時,負載由理想空載增加到額定值所對應的轉速降落△nN與理想空載轉速n0之比便是靜差率S,即
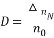 (1.3) (1.3)
顯然,靜差率是用來衡量調速系統在負載變化下轉速的穩定度的。 當然,調速范圍和靜差率兩項指標并不是孤立的,必須同時提出才 意義。在調速過程中,若額定轉速降相同,靜差率的大小與轉速的大小相關。如果低速時的靜差率滿足要求,那么高速時靜差率就更滿足要求了。因此,調速系統的靜差率指標應以最低轉速時所能達到的數值為準。 那么它們兩者之間存在什么關系呢? 一般以電動機的額定轉速nN作為最高轉速,若定負載下的轉速降落為△Nn,則 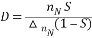 (1.4) (1.4)
可見,如果對靜差率的要求越高,即S越小時,系統能夠允許的調速范圍也越小。所以一個調速系統的調速范圍是在最低轉速時還能滿足靜差率的轉速可調范圍。 1.3轉速閉環直流調速系統的組成 具有轉速負反饋直流電動機調速系統的原理圖如圖1.2所示。 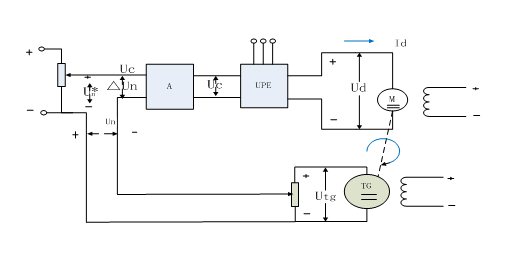
圖1.2 帶轉速負反饋直流電動機調速系統的原理圖 其中,被調量是轉速n,給定量是給定電壓Un*,測速發動機TG可以得到與被測轉速成正比的反饋電壓Un。UN*與UN相比較后,得到轉速偏差電壓△Un,經過比例放大器A,產生電力電子變換器UPE所需的控制電壓Uc。比例放大器又稱作比例(P)調節器。閉環控制系統和開環控制系統的主要差別就在于轉速n經過測量元件反饋到輸入端參與控制。 1.4 閉環系統的靜特性 電力電子變換器 Ud0=KsUc 直流電動機  電壓比例環節 △Un= Un*-Un 比例調節器 Uc=Kp△Un 測速反饋環節 Un=αn 式中: Ks—晶閘管整流器放大系數 Kp—比例調節器的比例放大系數 α—轉速反饋系數 從上述五個關系式中消去中間變量整理得到轉速負反饋直流調速系統的靜特性方程式 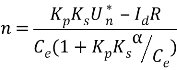 = =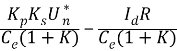 (1.5) (1.5)
式中 K—閉環系統的開環放大系數, 閉環系統的靜特性表示閉環系統電動機轉速與負載電流(或轉矩)間的穩態關系,它在形式上與開環機械特性相似,但本質上卻有很大的區別,故稱之為“靜特性”。
2.轉速閉環直流調速系統的動態數學模型2.1說明動態數學模型的推導步驟如果要分析系統的動態性能,需求出動態響應,為此,必須先建立描述系統動態物理規律的數學模型[2]。轉速閉環直流調速系統的動態數學模型的建立步驟可分為:將系統分為多個子系統,分別得到子系統的數學模型;根據各個子系統間的關系逐次得出輸入與輸出的關系,最終得到系統的數學模型。 2.2列寫簡單環節的數學模型轉速反饋控制直流調速系統中還有比較環節,放大環節、反饋環節,他們的響應都可以認為是瞬時的,因此他們的傳遞函數就是他們的放大系數。 比較環節:△Un(s)=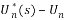 (s) (2.1) (s) (2.1) 放大環節:Wa(s) =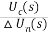 = Kp (2.2) = Kp (2.2) 反饋環節: Wfn(s) =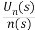 (2.3) (2.3) 2.3觸發整流環節數學模型的推導 晶閘管觸發和整流裝置的放大系數KS可由工作范圍內的特性斜率決定,計算公式為: 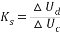 (2.4) (2.4)
在動態過程中,可把晶閘管觸發與整流裝置看成一個純滯后環節,其滯后效應是由晶閘管的失控時間引起的。由于晶閘管存在維持電流的特點,這就造成整流電壓滯后于控制電壓的狀況。 最大失控時間Tsmax是兩個相鄰自然換相點之間的時間,它與就留電源頻率和晶閘管整流器類型有關: 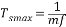 (2.5) (2.5)
式中 f—交流電源頻率 m—一周內整流電壓的脈沖數 在實際計算中一般采用平均失控時間Ts=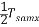 。 。 用單位階躍函數表示滯后,則晶閘管觸發與整流裝置的輸入與輸出關系為: 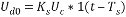 (2.6) (2.6)
利用拉普拉斯變換的位移定理,則晶閘管裝置的傳遞函數為 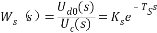 (2.7) (2.7)
將上式按泰勒級數展開得: 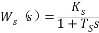 (2.8) (2.8)
2.4電動機環節的數學模型推導他勵直流電動機在額定勵磁下的等效電路如圖2.1所示。其中電樞回路總電阻R和電感L包含了電子變換器內阻,電樞電阻和電感及可能在主電路中接入的其他電阻和電感。 
圖2.1電動機等效電路 假如主電路電流連續,動態電壓方程為: 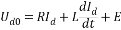 (2.8) (2.8)
若忽略粘性摩擦及彈性轉矩,電動機軸上的動力學公式為: 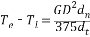 (2.9) (2.9)
式中 Tl—包括電動機空載轉矩在內的負載轉矩 GD2—電力拖動裝置折算到電動機軸上的飛輪慣量 額定勵磁下的感應電動勢和電磁轉矩分別為: 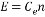 (2.10) (2.10)
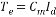 (2.11) (2.11)
式中 Cm—電動機額定勵磁下的轉矩系數,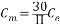 再定義下列時間常數: Tl—電樞回路電磁時間常數,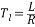 (2.12) (2.12) Tm—電力拖動系統機電時間常數,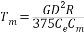 (2.13) (2.13) 整理后得: 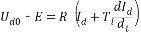 (2.14) (2.14)
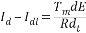 (2.15) (2.15)
式中 Idl—負載電流,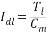 在零初始條件下,取等式兩側的拉普拉斯變換,得到電壓與電流間的傳遞函數為: 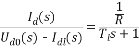 (2.16) (2.16)
電流與電動勢間的傳遞函數為: 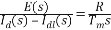 (2.16) (2.16)
分別畫出兩式的動態結構圖分別如圖 2.2 和圖2.3所示。 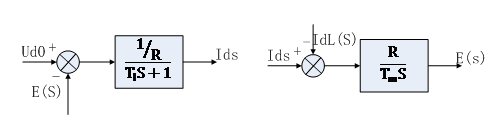
圖 2.2 圖 2.3 將兩圖合在一起,并考慮到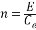 即得到額定勵磁下直流電動機的動態結構圖,如圖2.4 所示 
圖2.4 直流電動機的動態結構圖 由圖2.5 可知,額定勵磁下的直流電動機是一個二階線性環節,Tm和TL兩個時間常數分別表示機電慣性和電磁慣性。 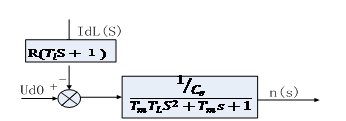
圖2.5 直流電動機的動態結構圖的變形 2.5轉速閉環直流調速系統的動態數學模型知道了各個環節的傳遞函數后 , 只需要按照系統中的相互關系組合, 便可畫出閉環直流調速系統的動態結構框圖, 如圖2. 6 所示。 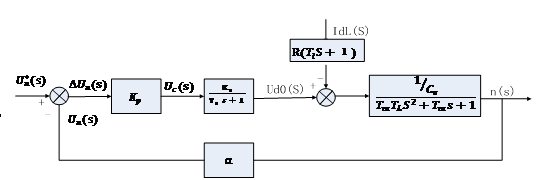
圖2. 6 閉環直流調速系統的動態結構框圖
3.系統動特性之穩定性分析3.1開環傳遞函數的獲得由圖2.6 可知,轉速反饋控制的直流調速系統的開環傳遞函數是 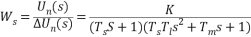 (3.1) (3.1)
式中,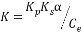 3.2閉環傳遞函數的獲得設IdL=0,從給定輸入作用看,轉速反饋控制直流調速系統的閉環傳遞函數是: 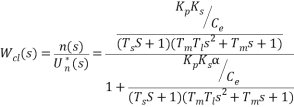
=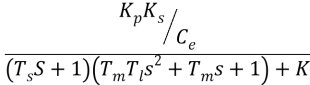 = 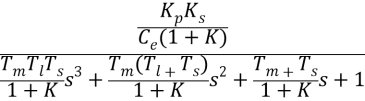 (3.2) (3.2) 3.3系統穩定對發達倍數K的要求根據勞斯穩定判據可知,放大倍數K應滿足 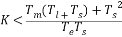 (3.3) (3.3)
3.4 一個例某龍門刨床工作臺拖動系統采用直流電動機,其額定數據如下;60KW,220V,305A,1000rpm,采用V-M系統,主電路總電阻R=0.18歐,電動機電動勢系數Ce=0.2V.min/r。 (1)如果要求調速范圍D=0,靜差率s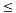 5%,采用開環調速能否滿足?若要求滿足這個要求,系統的額定速降 5%,采用開環調速能否滿足?若要求滿足這個要求,系統的額定速降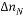 最多能有多少? 最多能有多少? (2)龍門刨床D=20, s≤5%,已知Ks=30,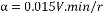 ,Ce=0.2V.min/r,采用比例控制閉環調速系統滿足上述要求時,比例放大器的放大系數應該有多少? ,Ce=0.2V.min/r,采用比例控制閉環調速系統滿足上述要求時,比例放大器的放大系數應該有多少? (3)若題(2)中,系統采用的是三相橋式可控整流電路,已知電樞回路總電阻R=0.18歐,電感量L=3mh,系統運動部分的飛輪慣量GD2=60N.m2,試判別系統的穩定性。 解:由題意得 (1)當電流連續時,V-M系統的額定速降為 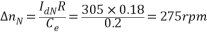
開環系統在額定轉速時的靜差率為 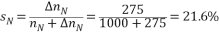
可見在額定轉速已不能滿足s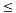 5%的要求,更不要說最低速了 5%的要求,更不要說最低速了 如要求D=20,s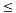 5%,即要求 5%,即要求 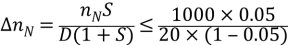 =2.63rpm =2.63rpm
可見,開環調速系統的額定速降太大,無法滿足D=20,S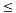 5%的要求,采用轉速反饋控制的直流調速系統將是解決此類問題的一種方法。 5%的要求,采用轉速反饋控制的直流調速系統將是解決此類問題的一種方法。 (2)由(1)可知,開環系統額定速降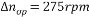 ,若為了滿足要求,閉環系統額定速降應為 ,若為了滿足要求,閉環系統額定速降應為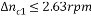 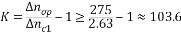
帶入已知參數,則得 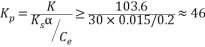
即只要放大器的放大系數等于或大于46,閉環系統就能夠滿足所需的穩態性能指標。 (3)電磁時間常數 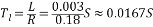 機電時間常數 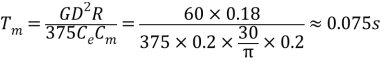 對于三相橋式整流電路,晶閘管裝置的時間滯后時間常數為 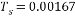 為了保證系統穩定,開環放大西沙胡應滿足式(3.3)的穩定條件: 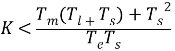 = =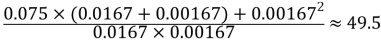
按動態穩定性要求K<49.5。但在題(2)中應有K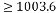 ,因此這樣的比例控制閉環系統的動態穩定性和穩定性能要求時矛盾的,所以該系統是不穩定的。 ,因此這樣的比例控制閉環系統的動態穩定性和穩定性能要求時矛盾的,所以該系統是不穩定的。
4.結論變壓調速是直流調速系統的主要調速方法,系統的硬件結構至少包含兩個部分:能夠調節直流電動機電樞電壓的直流電源和產生被調速的直流電動機。用可控直流電源和直流電動機組成一個開環直流電動機調速系統時,它的性能是不能很好的滿足期望值的。因此可以設計一個具有轉速反饋控制的直流電動機調速系統,但存在一個問題,假如只是簡單滿足了靜差率以及調速范圍,那么系統可能是不穩定的,因此設計時需要充分分析系統需求,以及系統穩定的條件,選擇適當的電子器件。
完整的Word格式文檔51黑下載地址:
 小論文.1 .docx
(721.98 KB, 下載次數: 10)
小論文.1 .docx
(721.98 KB, 下載次數: 10)
2017-12-20 19:41 上傳
點擊文件名下載附件
下載積分: 黑幣 -5
|