2017年11月20
撰寫了有關數字識別人工智能的課程設計論文,包括程序
手寫數字識別 摘要 手寫數字識別是機器學習領域中一個經典的問題,是一個看似對人類很簡單卻對程序十分復雜的問題。很多早期的驗證碼就是利用這個特點來區分人類和程序行為的。在手寫數字識別中,比如,我們要識別出一個手寫的“9”,人類可能通過識別“上半部分一個圓圈,右下方引出一條豎線”就能進行判斷。但用程序表達就似乎很困難了,你需要考慮非常多的描述方式,考慮非常多的特殊情況。在本文中將從K-近鄰算法(KNN)和一對多的邏輯回歸算法角度進行分析。
第1章 K-近鄰算法 最簡單最初級的分類器是將全部的訓練數據所對應的類別都記錄下來,當測試對象的屬性和某個訓練對象的屬性完全匹配時,便可以對其進行分類。但是怎么可能所有測試對象都會找到與之完全匹配的訓練對象呢,其次就是存在一個測試對象同時與多個訓練對象匹配,導致一個訓練對象被分到了多個類的問題,基于這些問題呢,就產生了KNN。 1.1 K-近鄰基本原理 KNN算法是從訓練集中找到和新數據最接近的k條記錄,然后根據它們的主要分類來決定新的數據的類別。具體算法步驟如下: ⑴ 算距離:給定測試對象,計算它與訓練集中的每個對象的距離。什么是合適的距離衡量?距離越近意味著這兩個點屬于同一類的可能性越大。其中距離的衡量方法包括歐氏距離、夾角余弦等。 ⑵ 找鄰居:圈定距離最近的k個訓練對象,作為測試對象的近鄰。 ⑶ 做分類:根據這k個近鄰歸屬的主要類別,來對測試對象分類。分類的判定可以是少數服從多數,在上個步驟的k個訓練對象中,哪個類別的點最多就分為該類。 1.2 matlab算法實現 本文中的訓練樣本為數字“0~9”,每個數字分別有500個樣本圖片,其中前400個樣本作為訓練集,后100作為測試集。訓練集已經根據數字進行分類,并且每個圖片都經過處理轉化為20×20的灰度矩陣。為了計算機方便計算,將20×20的灰度矩陣化成1×400的向量形式。 %% 初始化 clear; clc; k = 7; %設置找近鄰所需對象的數量 load labels load trainData [m,n] = size(trainData); %% testData a = 4; %a為第a類樣本 b = 56; eval(sprintf('load C:/Users/HP/Documents/%d_%d.txt',a,b)); eval(sprintf('testData = X%d_%d;',a,b)); testData = testData';
|
|
至此我們的測試樣本保存在testData中,接下來運行KNN算法。在執行KNN算法之前還需要對參數進行進行歸一化處理: D = max(trainData,[],2) - min(trainData,[],2); trainData = (trainData-repmat(min(trainData,[],2),1,n))./repmat(D,1,n); testData = (testData - min(testData))./(max(testData)-min(testData)); |
|
之后調用KNN算法,并顯示判斷結果: relustLabel = knn(testData,trainData,labels,k); fprintf('the real number in the picture is %d\n',a); fprintf('predict number in the picture is %d\n',relustLabel); |
|
算法具體代碼如下: function relustLabel = knn(inx,data,labels,k) % inx為測試集,data為訓練集,labels為訓練集標簽,k為判斷時選取的點的個數 % relustLabel為測試集的標簽 [datarow,datacol] = size(data); [inxrow,inxcol] = size(inx); data = repmat(data,1,1,inxrow); inx = repmat(reshape(inx',1,inxcol,inxrow),datarow,1,1); dis = reshape(sum((data-inx).^2,2),datarow,inxrow); [kdis,ind] = sort(dis,1); %¶Ô¾àÀëÅÅÐò ind = ind(1:k,:); for i = 1:inxrow, aa = tabulate(labels(ind(:,i))); [bb,inds] = max(aa(:,2)); relustLabel(i,:) = aa(inds) ; end |
|
程序運行結果如下 1.3 小結 KNN算法簡單易于理解,易于實現,無需參數估計,無需訓練。但它屬于懶惰算法,對測試樣本分類時的計算量大,內存開銷大,評分慢。可解釋性差。其結果會受到K取值的影響。近鄰中可能包含太多的其它類別的點。偶爾會出現錯誤,例如:
第2章 一對多的邏輯回歸 2.1 基本原理 在分類問題中,如果要預測的變量是一個離散的值,我們將利用到邏輯回歸的算法。對于一個二分類問題,我們可以利用Sigmoid函數來逼近我們的模型。函數圖像如圖所示: 此處 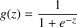 。Z可以看作是樣本的分界函數,我們要對訓練集做的工作就是訓練出一條合理的分界函數 。Z可以看作是樣本的分界函數,我們要對訓練集做的工作就是訓練出一條合理的分界函數 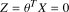 。在測試時,將測試樣本的X帶入得到Z的值,當Z大于0時屬于“1”類,當Z小于“0”時屬于“0”類。但在手寫識別中,我們的訓練樣本一共有10類。故采用一對多的分類方法。我們將多個類中的一個類標記為正向類(y=1),然后將其他所有類都標記為負向類,這個模型記作 。在測試時,將測試樣本的X帶入得到Z的值,當Z大于0時屬于“1”類,當Z小于“0”時屬于“0”類。但在手寫識別中,我們的訓練樣本一共有10類。故采用一對多的分類方法。我們將多個類中的一個類標記為正向類(y=1),然后將其他所有類都標記為負向類,這個模型記作 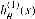 。接著,類似的我們選擇另一個類標記為正向類(y=2),再將其他類都標記為負向類,將這個模型記為 。接著,類似的我們選擇另一個類標記為正向類(y=2),再將其他類都標記為負向類,將這個模型記為 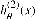 ,依此類推。最后我們得到十條不同的分界函數。 ,依此類推。最后我們得到十條不同的分界函數。 在測試過程中,我們將測試樣本的X分別帶入這十個分界函數  中得到Z1,Z2,Z3…Z10。若ZK>0,而其他Z都不大于0,則測試樣本屬于第k類。若有多個Z值都大于0則取最大的。 中得到Z1,Z2,Z3…Z10。若ZK>0,而其他Z都不大于0,則測試樣本屬于第k類。若有多個Z值都大于0則取最大的。 2.2 matlab算法實現 2.2.1數據處理
clear; clc;
%% 讀取數據 load ex3data1.mat; for i = 1:10 % 每個數字讀取前400個樣本 X_train([400*i-399:400*i],:) = X([500*i-499:500*i-100],:); y_train([400*i-399:400*i],:) = y([500*i-499:500*i-100],:); end m = size(X_train,1); class_y = zeros(m,10); X_train = [ones(m,1),X_train]; %將X擴展 n = size(X_train,2); initial_theta = zeros(n,1); |
|
2.2.2調用matlab中的優化工具箱 在邏輯回歸中代價函數為: 在設計代價函數的時候,為了避免出現過擬合的情況,我們往往加入了正則化,新的代價函數如下: 這樣在最小化代價 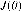 時,會讓 時,會讓 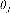 的二次項盡可能小,從而避免的過擬合的情況。 的二次項盡可能小,從而避免的過擬合的情況。 要求代價 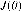 最小時的 最小時的  值,于是我們調用優化工具箱fminunc: 值,于是我們調用優化工具箱fminunc: %% 調用優化工具箱 options = optimset('GradObj', 'on', 'MaxIter', 400); lamda = 0.1; for i = 1:10; class_y(find(y_train==i),i) = 1; [theta(:,i),cost(i)] = fminunc(@(t)(costfun(t,X_train,class_y(:,i),lamda)),initial_theta,options); end |
|
其中costfun函數如下所示: function [J,grad] = costfun(theta,X,y,lamda) m = size(X,1); Z = X*theta; H = sigmoid(Z); J = -1*sum(y.*log(H)+(1-y).*log(1-H))/m+lamda/(2*m)*sum(theta(2:end).^2); thetaj = theta; thetaj(1) = 0; grad = (X'*(H-y)+lamda*thetaj)/m; end |
|
2.2.3 測試 讀取上一步保存的訓練參數thetazhenze。取一個測試樣本,帶入到 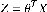 判斷Z的大小。 判斷Z的大小。 load thetazhenze; load ex3data1.mat; m = size(X,1); X = [ones(m,1),X]; i = 9;n = 50; %n作為偏移量在1:100中取,i作為數字類在0:9中取 H = X(500*(i+1)-100+n,:)*theta; [h,ind] =max(H); %取H中最大的標簽 if ind == 10, ind = 0; end fprintf('the number is %d\n',ind) %輸出結果 |
|
2.2.4 輸出結果 ① 若未加入正則化,當i等于9時輸出為8,發生錯誤: ② 若加入正則化,當i等于9時輸出為9,正確: 2.3 小結 一對多的邏輯回歸算法相比KNN算法增加了對訓練集的訓練過程,算法過程雖比KNN算法更復雜,但實際測試效果更理想。
第3章 總結 手寫數字識別的方法還有許多,例如可以用神經網絡進行識別。但時間有限,目前只用了這兩種方法,并用代碼實現,識別的準確率還有待提高。
完整的Word格式文檔51黑下載地址:
 自研1703班滕翔模式識別.docx
(142.52 KB, 下載次數: 15)
自研1703班滕翔模式識別.docx
(142.52 KB, 下載次數: 15)
2017-12-19 16:18 上傳
點擊文件名下載附件
模式識別
|